Порівняння множин 1

§ 6. Порівняння множин. Рахункові безлічі. 62

6.1. Поняття потужності множини 62

6.2. Рахункові безлічі 64

6.3. Незчисленних множин 67

Поняття потужності множини

Засновником вчення про множини є німецький математик Георг Кантор (G. Kantor, 1845-1918), професор з Галле. Однією з великих заслуг Кантора є те, що він встановив точні поняття, що виникають в завданні сравененія нескінченних множин за величиною або за обсягом. Це завдання є тривіальною для кінцевих множин і вирішується порівнянням кількостей елементів у них. Але для нескінченних множин завдання їх порівняння призводить до непростої проблеми: чи можна нескінченну кількість елементів однієї множини вважати великим, рівним або меншим безкінечного кількості елементів іншого безлічі? За пропозицією Кантора, порівняння двох множин здійснюється взаємно однозначної відповідності між їх елементами.

Кажуть, що між елементами двох множин

іможна встановити взаємно однозначну відповідність (біекція), якщо:

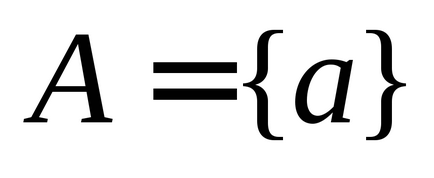
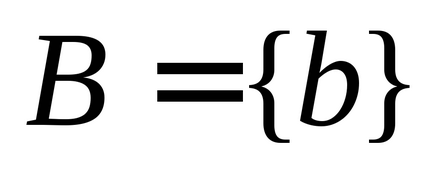
1) кожному елементу

відповідає єдиний елемент

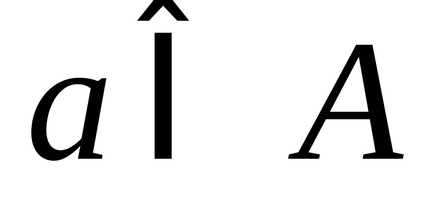
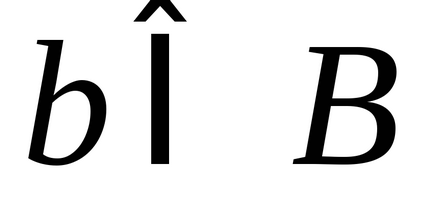
2) кожен елементами

є відповідним єдиному елементу.

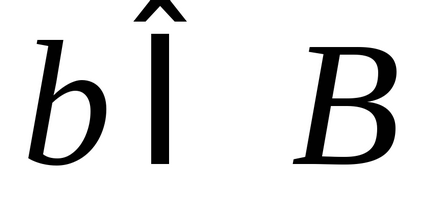
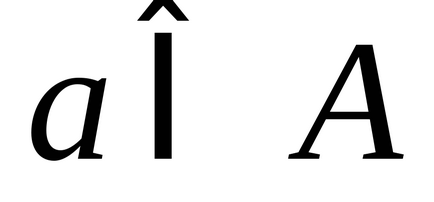
Визначення еквівалентних (рівнопотужних) множин

Два безлічі, між елементами яких можна встановити взаємно однозначну відповідність (біекція), називаються рівнопотужними множинами. або множинами, що мають однакову потужність. або еквівалентними множинами по потужності.

Позначення еквівалентних (рівнопотужних) множин:

Таким чином, між елементами рівнопотужних (еквівалентних) множин завжди існує биективное відображення. Якщо ж таке відображення встановити неможливо, то безлічі мають різну потужність. при цьому виявляється, що яким би чином ми не намагалися привести у відповідність елементи обох множин, завжди залишаться зайві елементи і притому завжди від одного і того ж безлічі, яке має тому «велику потужність». Наприклад, очевидно, що дві кінцевих безлічі рівнопотужні тоді і тільки тоді, коли вони містять однакову кількість елементів.

Приклад (еквівалентні кінцеві безлічі)

де

і - це кількості елементів в кінцевих множинах і .

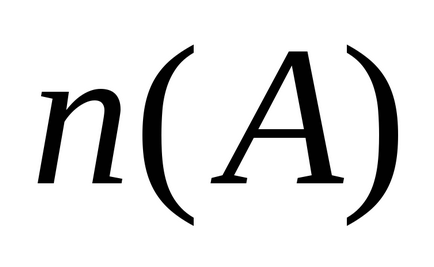
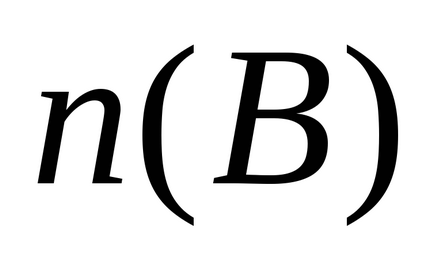
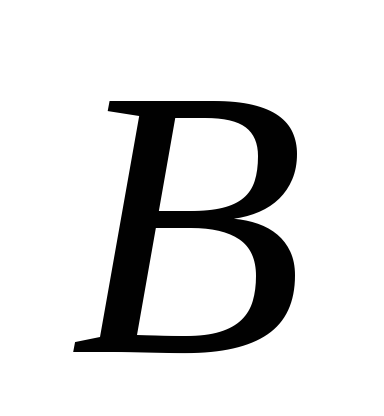
Безліч, яке не є кінцевим, називається нескінченним і кількість елементів в ньому не може бути виражено ніяким числом. Тому порівняти нескінченні безлічі можна тільки по їх потужності, тобто за допомогою процедури, яка встановлює взаємно однозначну відповідність між елементами цих множин.

Також очевидно, що:

1) з двох кінцевих множин

і , в яких, велику потужність має безліч, що містить більшу кількість елементів.

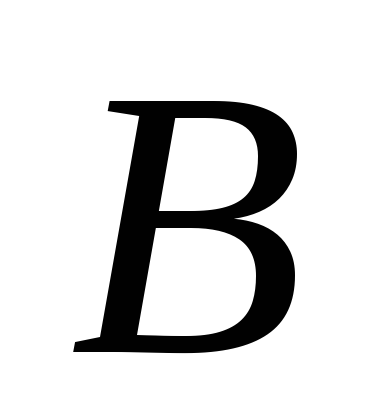
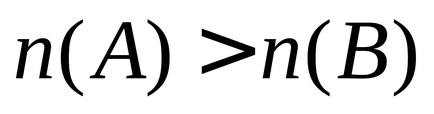
2) будь-яке кінцеве безліч

завжди має більшу потужність, ніж будь-яке його власне підмножина.

Приклади (еквівалентні нескінченні безлічі)

т. е. множествоN всіх натуральних чисел має таку ж потужність, як і його власна частина, що складається тільки з парних чисел.

2) т. Е. Безліч

всіх цілих чисел і множина всіхнатуралних чисел мають однакову потужність.

безлічі

і еквівалентні (мають однакову потужність), так як між їх елементами легко встановлюється відповідність так, як показано на малюнку 1, таким чином, безлічі точок на відрізках різної довжини мають однакову потужність (рис.36).

)

, так як між елементами цих нескінченних множин встановлюється взаємно однозначна відповідність, наприклад, за допомогою графіка функції , (Рис. 37)

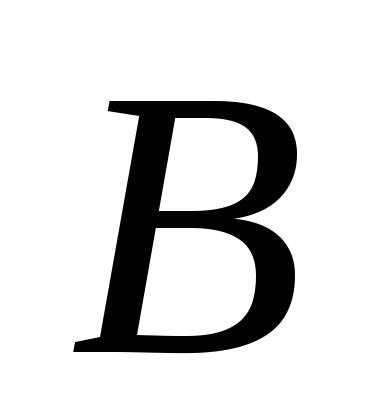
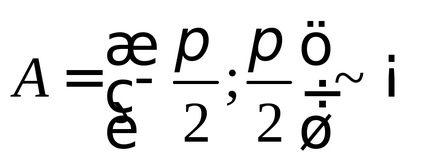
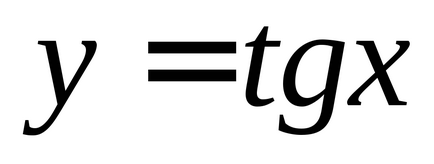
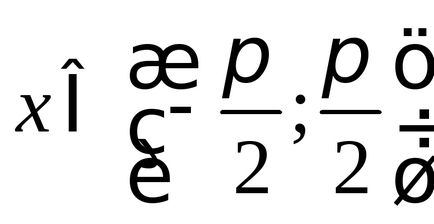
(Рис. 2), таким чином, безліч

всіх дійсних чисел має однакову потужність з безліччю точок інтервалу .

Розглянуті приклади переконливо показують, що власна частина (власне підмножина) нескінченної кількості може мати рівну з ним потужність, тобто для нескінченних множин не є вірним твердження «частина менше цілого».

Схожі статті

• Порівняння фіат добло і ваз largus

• Порівняння шевроле Каптіва і ніссан х-трейл

• Порівняння ауді Ку3 і Міцубісі АСХ