Модель 1. Система постулатів Евкліда
Постулати 1-3 визначають можливість побудов лінійкою (без поділів) і циркулем. Корисно уточнити, що під «прямий» Евклід розуміє «обмежену» пряму, тобто, в сучасній термінології, відрізок.
Математики багаторазово зверталися до системи постулатів і аксіом Евкліда, намагаючись поліпшити її. Так, в XVIII в. було усвідомлено, що постулат 4 є зайвим, оскільки випливає з інших постулатів і аксіом.
Подібні дослідження тривалий час велися і щодо 5-го постулату, тим більше, що він, через складність формулювання, здавався набагато менш очевидним, ніж інші постулати і аксіоми. Його намагалися довести, виходячи з інших постулатів і аксіом. При цьому з'ясувалося тільки, що 5-й постулат логічно еквівалентний деяким іншим твердженням (тобто вони можуть бути виведені з нього, а з іншого боку, він сам може бути виведений з будь-якого з них, якщо вважати їх уже встановленими), але ні він , ні ці твердження не можуть бути доведені на основі інших постулатів і аксіом Евкліда. Мислима геометрія, в якій 5-й постулат не виконується, а решта постулати і аксіоми виконуються (геометрія Лобачевського). Зазвичай в сучасних викладах геометрії 5-й постулат замінюється на еквівалентну йому аксіому паралельних (зустрічається вже у Прокла в V ст. Н. Е.): Через точку, що не лежить на даній прямій, можна провести тільки одну пряму, що не перетинається з цією. (Слово «пряма» тут, як завжди в сучасній математиці, позначає нескінченну пряму).
Модель 2. Аксіома паралельності
Списки аксіом Евкліда в різних збережених старовинних копіях «Начал» відрізняються один від одного - можливо, не всі наведені там аксіоми (та й постулати) належать самому Евклиду. Найпоширенішим є наступний список аксіом.
Рівні одному і тому ж рівні і між собою.
І дві прямі не містять простору.
Природне запитання, що виникає при знайомстві з постулатами і аксіомами Евкліда, - ніж постулати відрізняються від аксіом. В цілому слід розуміти, що аксіоми, на відміну від постулатів, стосуються дуже загальних властивостей величин самої різної природи, в т. Ч. Наприклад, чисел, а не тільки геометричних об'єктів. Проте, аксіома 9 суперечить такій інтерпретації. Сенс цієї аксіоми - в тому, що два відрізки не можуть сходитися в двох різних точках - тобто обмежувати деяку фігуру кінцевої площі.

Мал. 1. Дев'ята аксіома Евкліда
Ми б зараз сформулювали цю аксіому так: «Через дві точки проходить не більше однієї прямої». Спробуйте зрозуміти, в чому відмінність даної аксіоми від постулату 1?
Постулат 1 стверджує існування принаймні одного відрізка з кінцями у двох даних точках, а аксіома 9 - те, що таких відрізків не більше одного.
Важливу роль відіграє аксіома 7. Фактично, мова в ній йде про те, що якщо накласти одну фігуру на іншу так, що вони співпадуть, то ці фігури будуть рівні. Евклід завжди вживає слово «рівні» в сенсі равновеликости, т. Е. Рівності площ (довжин, об'ємів, величин кутів). У сучасному розумінні слово «рівні» в застосуванні до геометричних фігур означає саме «збіг при накладенні»: рівні фігури відрізняються тільки місцем розташування (вірніше, рівність означає, що існує рух, що переводить одну фігуру в іншу; під рухом розуміється перетворення, що зберігає відстань, як якби фігура була твердою і ми могли б її рухати). Уже математики XVII в. розуміли рівність саме в цьому сенсі; Г. В. Лейбніц для такого рівності ввів спеціальний термін - конгруентність. Так що аксіома 7, в сучасних термінах, означає, що рівні (неконгруентні) фігури рівновеликі. (При цьому, зрозуміло, рівновеликі фігури не зобов'язані бути рівними).
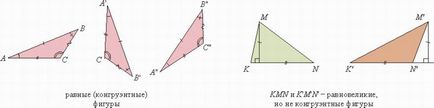
Мал. 2. Рівновеликі і рівні фігури
За допомогою «суміщення» Евклід доводить те, що зараз називається ознаками рівності трикутників, але в подальшому він уникає суміщень, посилаючись при доказі рівності тих чи інших фігур на вже доведені ознаки рівності трикутників.
В цілому, вибір постулатів і аксіом у Евкліда вдалий, але його система не є повною: у ній відсутні багато важливих аксіоми (наприклад, стереометричні). Втім, ще Аристотель вважав, що іноді викладу тієї чи іншої науки обходять мовчанням деякі властивості і положення внаслідок їх очевидності. Цілком можливо, що Евклід не ставив собі за мету дати повний список тверджень, необхідних для подальших доказів. Це завдання він залишив наступним математикам.