У методі LU-факторизації (цю схему називають компактною схемою Гаусса) при вирішенні системи виконується наступна послідовність дій.
Матриця представляється у вигляді добутку
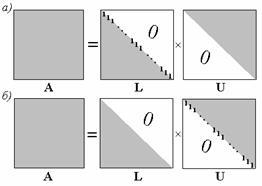
Мал. 2.3. Структура матриць L і U в розкладах Дулиттла (а) і Краута (б)
де L - нижня трикутна матриця, U - верхня трикутна матриця. Таке розкладання єдине за умови попереднього вибору діагональних елементів однієї з матриць. У цьому випадку число елементів в матриці A збігається з сумарним числом невідомих елементів матриць L і U. Якщо діагональ L приймається одиничною, то таке розкладання називають розкладанням Дулиттла (рис. 2.3, а), якщо одинична діагональ U - розкладанням Краута (рис. 2.3 , б). Надалі при побудові методу LU- факторизации будемо залучати розкладання Краута.
Система замінюється системою
легко розв'язуваної за два кроки:
Крок 1. . Беручи до уваги трикутний вид матриці L. неважко отримати, що в алгоритмі Краута
Крок 2.. Вирішення цієї системи в алгоритмі Краута:
Сумарні витрати реалізації обох кроків при n >> 1 складають довгих операцій.
Отримаємо співвідношення для розрахунку елементів матриць L і U в алгоритмі Краута. Для цього перемножимо матриці L і U і прирівняємо результат до A. За правилом множення матриць
Розглянемо елемент (рис. 2.4), розташований на центральній діагоналі або в нижній трикутної частини матриці A. Для такого елементаi ≥ j. З малюнка слід, що
Мал. 2.4. Ілюстрація обчислення елемента матриці, розташованого
нижче головної діагоналі
так як i ≥ j і. Звідси
Розглянемо елемент (рис. 2.5), що знаходиться вище за головну
Мал. 2.5. Ілюстрація обчислення елемента матриці, розташованого
вище головної діагоналі
діагоналі матриці A (для нього j> i). В цьому випадку
Отримали в результаті співвідношення, які дозволяють обчислювати елементи матриць L і U. Послідовність обчислень: спочатку обчислюється стовпець матриці L. далі рядок матриці U. потім знову стовпець матриці L. далі рядок матриці U і т. Д. (Див. Рис. 2.6, який ілюструє послідовність обчислень і схему зберігання матриць L і U).
Обчислення стовпця матриці L і рядки матриці U назвемо кроком LU-розкладання. Наведемо як приклад схему зберігання елементів матриць A, L, U після другого кроку LU-розкладання (рис. 2.7).
Число довгих арифметичних операцій на етапі LU-розкладання при n >> 1 становить величину. на кроці рішення ли
лінійних систем з трикутними матрицями -. Сумарне число довгих операцій приблизно дорівнює (як і в методі Гаусса),
Мал. 2.6. Вихідна матриця A (а), схема зберігання L і U матриць (б), послідовність обчислення елементів в прийнятій схемі зберігання (в)
Мал. 2.7 Схема зберігання елементів 4'4 матриць A, L, U після другого кроку LU-факторизації
т. е. основні витрати припадають на LU-факторизації матриці A. Ця особливість робить особливо привабливим метод LU-факторизації при вирішенні СЛАР з однієї і тієї ж матрицею A. але різними правими частинами:
В цьому випадку факторизация матриці виконується одноразово, вимагаючи довгих операцій, а рішення кожної системи з відповідною правою частиною реалізується за таких операцій.
Виключно ефективну реалізацію методу LU-факторизації можна отримати, якщо обмежитися класом лінійних систем із симетричною позитивно певної матрицею A. т. Е. Таку реалізацію називають методом Холесского, або методом квадратного кореня.
Будемо вважати, що розв'язувана система
має симетричну позитивно певну матрицю A. В цьому випадку матриця A представляється у вигляді
Тут - нижня трикутна матриця. Таке розкладання існує і єдино для позитивно певних симетричних матриць.
Система перетвориться до виду
Вектор шукається шляхом послідовного вирішення двох систем з трикутними матрицями:
Для отримання розрахункових співвідношень елементів матриці розглянемо довільний елемент матриці A:
Підсумовування тут виконується тільки до j. т. к. j≤i. Виділимо член при значенні k = j:
Ці співвідношення дозволяють обчислити за стовпцями елементи матриці.
Ефективність такого методу досягається на етапі розкладання матриці, т. К. Необхідно обчислити в цьому випадку тільки матрицю. Арифметичні витрати в методі Холесского складають довгих операцій і n операцій добування квадратного кореня.
Існує інший варіант розкладу симетричної позитивно певної матриці, в якому вдається уникнути операцій добування квадратного кореня. У цьому варіанті вводиться нова матриця за правилом
причому - матриця, обчислена раніше за схемою Холесского, - діагональна матриця з елементами матриці. Матриця існує і є нижньою трикутною з одиничною діагоналлю. В цьому випадку
Розрахункові співвідношення для елементів матриць і можна отримати, як і раніше, залучаючи правило множення матриць
з якого випливає, що
т. к. матриця має одиничну діагональ.
Такий алгоритм зажадає вдвічі більшого числа перемноження, ніж схема Холесского. Однак, якщо ввести заміну змінних
то розрахункові співвідношення візьмуть вид
Тут спочатку обчислюють допоміжні величини. а потім їх використовують для визначення шуканих величин і. Кількість умножений при такій організації алгоритму становить приблизно і не містить операції вилучення квадратного кореня.