Метод факторизації матриць
Одним з найбільш ефективних методів відновлення 3D форми і руху об'єкта є метод, заснований на факторизации матриць. Пояснимо суть методу для лінійних наближень. Вище було показано, що рівняння, що описують лінійні наближення, мають вигляд (2.3.20):
Сформуємо з координат матрицю вимірювань W розміру 2F x P:

Кожен рядок матриці W містить координати точок (ufp, vfp), що відносяться до певного кадру послідовності, а кожен стовпець, - ті ж величини для конкретної точки, яка присутня на всіх зображеннях. Тоді вираз (2.3.33) можна переписати в матричній формі:
де M - матриця руху (орієнтації камер) розміру 2F x 3, S - матриця форми (точки на об'єкті), розміру 3 x P, T - вектор трансляцій камер (положення камер в просторі), розміру 2F x 1, що формуються наступним чином:

Помістимо початок МСК в ЦМ точок об'єкта (2.3.10):
Зауважимо, що вектор T можна отримати порядковим підсумовуванням елементів матриці W:
тоді далі будемо працювати з матрицею W *:
Оскільки матриця W * подана в вигляді твори матриці M розміру 2F x 3 і матриці S розміру 3 x P, її ранг не може бути більше 3. У даній роботі виконання факторизации рангу 3 матриці W, здійснювалося за допомогою сингулярного розкладання матриць (SVD):
тут U, V - ортогональні матриці, а У = diag (у1, ..., уn), n = min (2F, P), у1, ..., уn - сингулярні числа матриці W. Впорядкуємо все сингулярні значення за спаданням, і виберемо з матриці У верхню підматрицю розміру 3 x 3, значеннями якої будуть 3 максимальних сингулярних числа, що відповідають основним компонентам матриці W. Тоді, вибираючи з матриць U і V подматріци з рядків, що відповідають трьом найбільшим сингулярним числах, отримуємо апроксимацію до матриці W. Зрозуміло, що таке розкладання не єдиний, оскільки межу матрицями M) і S) завжди можна вставити про Зведення прямого і зворотного матриць Q рангу 3, нічого при цьому не змінивши, тоді можна записати:
Тут М і S мають на увазі справжні матриці руху і форми.
отримаємо такі системи рівнянь для наближень для знаходження матриці Q:
Де значення і відповідають таблиці 2.3.2. (Див. Також табл. 2.3.1)

У даній роботі системи (2.3.41) вирішувалися методом найменших квадратів (МНК) із застосуванням SVD.
Неоднозначність відновлення форми сцени пов'язана з тим, що в завдання легко можна внести знакову неоднозначність, замінивши матрицю Q на наступну матрицю:
Зафіксувавши орієнтацію осей системи координат, наприклад, вибравши напрямок осей таким же, як у системи, пов'язаної з однією з камер, неоднозначність в перших двох знаках можна усунути. З огляду на вирівнювання по першій камері, отримаємо шукані матриці руху і форми:
Неоднозначність в третьому знаку пов'язана з тим, що у всіх розглянутих нами лінійних наближень, глибиною об'єкта в порівнянні з відстанню до нього нехтують (відбувається так зване "сплощення" сцени). Як наслідок, це призводить до неоднозначності відновлення форми сцени S і руху камер M.
Ітераційний метод вирішення 3D-завдання
Основними недоліками розглянутих вище лінійних наближень, є неоднозначність у визначенні знака глибини сцени і неможливість обчислення фокусних відстаней камер. Наявність на зображеннях перспективних спотворень є додатковим джерелом інформації, що дозволяє усунути перераховані недоліки.
Оскільки метод точний, він описується уравнеіямі (2.3.39), в яких ми вважаємо g постійним для всіх кадрів.
Перепишемо (2.3.44) у вигляді, використовуючи вже зустрічалося заміну zf на zf ':
Таким чином, права частина отриманих рівнянь відповідає правій частині рівнянь для МОП (2.3.17), а ліва представляє собою суму лівій частині лінійних наближень і добавки. У матричної формі отримаємо тепер:

Тобто матриця W представлена у вигляді двох доданків, перше з яких, W1, відповідає введеної раніше матриці вимірів, а друге, W2, залежить від W1, sp, kf, і має сенс поправки на перспективні спотворення:
Як було показано раніше, ранг правій частині (2.3.45) завжди дорівнює 3, тому пропонується по итерациям підбирати параметр б, використовуючи відомі з попереднього кроку значення sp, kf, таким чином, щоб зберегти рівність рангів обох частин (2.3.45). Отже, система рівнянь (2.3.45) може бути вирішена ітераціями, шляхом уточнення поправочний матриці.
Запропонований ітераційний алгоритм добре працює в разі центрального наведення на об'єкт, внаслідок того, що в якості початкового наближення обрана МОП - проекція. Якщо є суттєва необхідність працювати строго в ситуації нецентрального наведення, доцільніше використовувати в якості 42
початкового наближення параперспектівную проекцію. Сформулюємо пропонований алгоритм рішення нелінійної задачі відновлення.
1. Вважаємо в (2.3.46) Номер ітерації q = 0, параметр б = 0, W (0): = W1, W2 (0): = 0.
2. Вирішуємо систему рівнянь, що описує МОП-наближення:
3. Вважаємо тепер: q: = q + 1.
4. Обчислюємо поправочний матрицю:
5. Знаходимо коефіцієнт б (q), підбираючи його таким, щоб ранг матриці W (q) залишався рівним 3, тобто треба шукати:
де у1, у4 - це перше і четверте сингулярні значення матриці W (q). Діапазон зміни параметра б (q) визначається з умови:
6. Оновлюємо матрицю
7. Переходимо до п.2, якщо одна з вимог виходу:
де значення е вибирається досить малим.
8. Усуваємо неоднозначність знака глибини сцени:
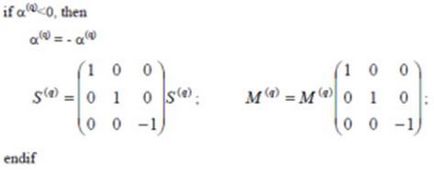
9. Вирівнюємо МСК по СК, пов'язаною з однією з камер.