Назва походить від грец. λημνίσκος - стрічка, пов'язка. У Стародавній Греції «лемніската» називали бантик, за допомогою якого прикріплювали вінок до голови переможця на спортивних іграх. Даний вид лемніскати названий на честь швейцарського математика Якоба Бернуллі. який поклав початок її вивчення.
Розглянемо найпростіший випадок: якщо відстань між фокусами дорівнює 2 c. розташовані вони на осі O X. і початок координат ділить відрізок між ними навпіл, то наступні рівняння задають лемніската:
Фокуси лемніскати - F 1 (- c; 0) (-c; 0)> і F 2 (c; 0) (c; 0)>. Візьмемо довільну точку M (x; y). Твір відстаней від фокусів до точки M є
і за визначенням воно дорівнює c 2>:
Зводимо в квадрат обидві частини рівності:
Розкриваємо дужки в лівій частині:
Розкриваємо дужки і згортають новий квадрат суми:
Виносимо загальний множник і переносимо:
Далі можна зробити заміну a 2 = 2 c 2 = 2c ^>. хоча це не обов'язково:
В даному випадку a - радіус кола, що описує лемніската.
Провівши нескладні перетворення, можна отримати явну рівняння: y = ± c 4 + 4 x 2 c 2 - x 2 - c 2 + 4x ^ c ^ >> - x ^ -c ^ >>>
Зводимо в квадрат і розкриваємо дужки:
Наводимо до виду
Взявши корінь і відкинувши варіант з негативним другим доданком, отримаємо:
де позитивний варіант визначає верхню половину лемніскати, негативний - нижню.
(Ρ 2 cos 2 φ + ρ 2 sin 2 φ) 2 = 2 c 2 (ρ 2 cos 2 φ - ρ 2 sin 2 φ) \ rho ^ \ cos ^ \ varphi + \ rho ^ \ sin ^ \ varphi ^ = 2c ^ \ rho ^ \ cos ^ \ varphi - \ rho ^ \ sin ^ \ varphi>
Використовуємо ще одне тотожність: cos 2 α - sin 2 α = c o s 2 α \ alpha - \ sin ^ \ alpha = cos2 \ alpha>:
Як і в випадку прямокутної системи можна замінити a 2 = 2 c 2 = 2c ^>:
Щільність точок кривої при рівномірному зміні параметра
Це єдиний варіант раціональної параметризації кривої. Рівняння повністю описує криву, коли параметр пробігає всю речову пряму. від - ∞ до + ∞. При цьому, коли параметр прагне до - ∞. точка кривої прагне до (0; 0) з другої координатної чверті. а коли параметр прагне до + ∞. то - з четвертої. Розподіл точок, які дає параметричне рівняння, при зміні його параметра з фіксованим кроком показано на малюнку.
Рівняння лемніскати в полярній системі
підставимо в формули переходу до полярної системі координат x = ρ cos φ. y = ρ sin φ. зведені в квадрат:
Розглянемо перше рівняння:
x 2 = 2 c 2 cos 2 φ cos 2 φ = 2c ^ \ cos 2 \ varphi \ cos ^ \ varphi>
Витягуємо корінь з обох частин рівності:
Якщо зробити заміну p 2 = tg (π 4 - φ) = \ operatorname \ left (> - \ varphi \ right)>. то отримуємо шуканий вираз для x:
Щоб задати лемніската за двома довільним точкам, можна не виводити рівняння заново, а визначити перетворення координат, при якому старий (даний) фокусний відрізок переходить в новий, і впливати на представлені рівняння цим перетворенням.
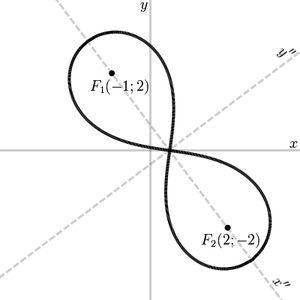
Нехай, наприклад, F 1 (- 1; 2). F 2 (2; - 2) (-1; 2), \, F_ (2; -2)> - фокуси.
Існує прямокутна система координат (на малюнку - x "O y"), в якій рівняння лемніскати має вигляд
Необхідно визначити перетворення системи координат, що переводить x O y в x "O y". Це перетворення здійснюється в два етапи: паралельний перенос і поворот.
Після перенесення системи координат її треба повернути на деякий кут. Для визначення кута спочатку знайдемо відстань між фокусами:
Тепер з геометричних міркувань знаходимо синус і косинус кута нахилу F 1 F 2 F_> до O X:
Поєднавши обидва перетворення, отримаємо кінцеві формули переходу:
Для того, щоб отримати рівняння в стандартній системі координат, підставимо ці співвідношення в вихідне рівняння кривої:
x 4 + y 4 + 24 xy - 2 xy 2 + 2 x 2 y 2 - 2 x 3 + 5 x 24 x - 3 y 2 - 12 y + 15 16 = 0 + y ^ + 24xy-2xy ^ + 2x ^ y ^ -2x ^ + 5x ^ -4x-3y ^ -12y +> = 0>
Це рівняння задає лемніската з фокусами F 1 (- 1; 2). F 2 (2; - 2) (-1; 2), \, F_ (2; -2)> в стандартній прямокутній системі координат.
За допомогою січних (спосіб Маклорена)
Будується коло радіуса c 2 >>> з центром в одному з фокусів. З середини O фокусної відрізка будується довільна січна O P S (P і S - точки перетину з колом), і на ній в обидва боки відкладаються відрізки O M 1> і O M 2>. рівні хорді P S. Точки M 1>. M 2> лежать на різних петлях лемніскати.
шарнірні методи
варіант перший
На площині обираються дві точки - A і B - майбутні фокуси лемніскати. Збирається спеціальна конструкція з трьох скріплених в ряд на шарнірах відрізків, щоб отримана лінія могла вільно згинатися в двох місцях (точки згину - C і D). При цьому необхідно дотримати пропорції відрізків: A C = B D = A B 2. C D = A B >>, \; CD = AB>. Краї лінії кріпляться до фокусів. При непараллельное обертанні відрізків навколо фокусів середина центрального відрізка опише лемніската.
варіант другий
У цьому варіанті лемніската будується по фокусу і подвійний точці - A і O відповідно. Збирається майже така ж шарнірна конструкція як і в попередньому варіанті, але прикріплений до подвійної точці відрізок O C з'єднується ні з кінцем центрального B D. а з його серединою. Пропорції також інші: B C = C D = O C = A O 2. A B = A O >>, \; AB = AO>.
Побудова лемніскати за допомогою січних