Кручення циліндричних стрижнів.
Розглянемо циліндричний стрижень (рис.1), бічні поверхні якого вільні від навантажень а до торцевих поверхонь прикладені моменти, спрямовані уздовж осьової лінії стержня. Ось спрямована уздовж осі стрижня.
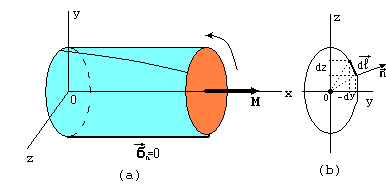
Рис.1 Крутіння стрижня моментом. На бічній поверхні сили не діють: вектор напружень дорівнює нулю.
Скористаємося рівняннями рівноваги пружного середовища при відсутності масових сил:
Рівняння (1) необхідно вирішити з однорідними (вектор напружень дорівнює нулю) граничними умовами на бічній поверхні, де вектор нормалі
На торцевій поверхні головний вектор сил має дорівнювати нулю, а головний момент заданий і має складову тільки на вісь. Звідси для складових головного вектора одержимо
для складових головного моменту маємо векторне умова
або три скалярних
Будемо вважати, що нормальні перетину стрижня залишаються плоскими і лише повертаються на кут пропорційний відстані між ними
Відмінними від нуля деформаціями і напруженнями будуть:
Відзначимо, що напруги тотожне задовольняють рівнянням рівноваги (1) і останнім двом граничним умовам (1), а їх підстановка в першу умову (2) дає співвідношення
де довільна точка бічній поверхні циліндра.
Умова (6) можна виконати тотожне тільки в тому випадку, якщо вважати перетин циліндра окружністю.
Умови (3) рівності нулю головного вектора сил
виконуються, якщо вісь проходить через центр ваги перерізу.
Умови (4) для моментів на торці циліндра візьмуть вид
Таким чином для стержня круглого перетину вдається побудувати рішення повністю, оскільки кут закрутки визначається першою умовою з (7):
де геометричний момент інерції перетину щодо осі
У загальному випадку, коли розтин не є колом його площину при крученні спотворюється, тому будемо шукати рішення для переміщень у формі
Тоді відмінні від нуля деформації і напруги такі:
умови рівноваги (1) призводять до рівняння для функції
Тоді умови (2) відсутність зусиль на бічній поверхні еквівалентні рівняння для точок контуру перетину
З огляду на, що для довільної точки контуру
перепишемо умова (11) у формі
Таким чином враховуючи рівняння (10) визначення функції крутіння звелося до вирішення завдання Неймана. Для функції, пов'язаної до гармонійної функції
. тобто виконані умови Коші-Рімана отримаємо з (12)
Тобто вийшла задача Діріхле. Постійна інтегрування для випадку багатозв'язних контурів перетину на кожному контурі приймає своє значення.
Якщо ввести функцію напружень, отримаємо
Функція напружень буде задовольняти рівняння Пуассона
з граничною умовою
на кожному з контурів перетину в разі його багатозв'язна.
Перевіримо умову рівності нулю головного вектора сил, прикладених на торцях стрижня. оскільки,
Знайдемо момент сил на торці стрижня
де площа обмежена критим контуром кордону многосвязной області перетину, причому для зовнішнього контуру а для інших контурів постійні визначаються з умови безперервності вектора переміщення при обході контуру.
При обчисленні інтеграла по внутрішнім контурам кордону враховано, що обхід контуру залишає область з лівого боку, а також те, що
де площа області, обмежена контуром.
Для однозв'язного контуру
для багатозв'язного контуру
Теорема про циркуляцію дотичного напруження. Визначення постійних для многосвязной області перетину контуру.
Теорема про циркуляцію дотичного напруження по будь-якому замкнутому контуру:
I =. де площа, обмежена контуром
При обчисленні циркуляції врахуємо формули (8) для переміщення
і формули (9) для напруг
В результаті підстановки напружень в вираз для циркуляції отримаємо:
Оскільки в силу однозначності переміщення при обході контура інтеграл
Застосовуючи теорему про циркуляцію до кожного внутрішнього контуру кордону многосвязной області, отримаємо систему рівнянь для визначення
Перевіримо отримані результати на прикладі контуру, обмеженого двома концентричними колами зовнішнього радіуса і внутрішнього радіусу.
Умова рівності нулю на зовнішній поверхні можна виконати, якщо шукати функцію напружень у вигляді
Після підстановки в рівняння Пуассона, отримаємо
Застосуємо теорему про циркуляцію до внутрішнього контуру
Таким чином дана функція напружень задовольняє всім умовам завдання.
Знайдемо діючий момент прямим обчисленням і використовуючи формулу (17):
Кручення циліндра з еліптичних перетином
Розглянемо циліндр, контуром перерізу якого є еліпс.
Будемо шукати функцію напружень у вигляді
яка на контурі очевидно дорівнює нулю. Її оператор Лапласа дорівнює
звідки знаходимо сонстанту В
Максимальна дотичне напруження досягається на кордоні і одно
Обчислюючи момент знайдемо його зв'язок з кутом кручення
Кручення стержня прямокутного перерізу.
Розглянемо кручення стержня прямокутного перерізу:
Будемо шукати функцію напружень у вигляді ряду
При такому розкладі на кордонах Підставами (20) в рівняння Пуассона
Помножимо ліву і праву частину рівності на і проинтегрируем по від до, з огляду на ортогональность функцій і, тобто
Облік (22) після інтегрування призводить до наступних рівнянь для функцій:
Обрано рішення, яке задовольняє умові
Таким чином функція напружень знайдена у вигляді ряду:
Знайдемо рішення іншим способом. Розглянемо прямокутник в якому. Тоді в силу граничних умов при можна шукати рішення у вигляді
В (24) функція буде задовольняти гармонійному рівняння. Якщо як і раніше вирішувати задачу методом поділу змінних, для функцій отримаємо однорідні рівняння
Оскільки нам потрібні парні рішення, отримаємо
Знайдемо постійні з умови. Для цього помножимо рівняння
на і проинтегрируем по від до.
В результаті отримаємо:
Відмінність рішення (25) від (23) істотно, оскільки частина ряду підсумувати і залишився ряд швидко сходиться.
Якщо знайти момент і максимальне дотичне напруження, отримаємо:
Для профілів у вигляді тонких смуг шириною і довжиною
а для відкритих профілів, складених з декількох смуг
Крутіння тонкостінного стержня багатозв'язного перетину.
Нехай перетин стрижня являє собою тонкостінну багатозв'язкову область (рис.2). Будемо вважати, що товщина багато менше радіуса кривизни
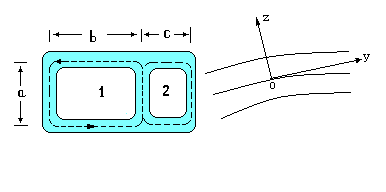
Мал. 2 Тонкостінний стрижень багатозв'язного перетину
Тоді для виділеного елемента стінки стрижня стінки можна вважати паралельними, а рішення слабо залежать від змінної. У цьому випадку рівняння Пуассона можна наближено записати у вигляді
Рішення рівняння (26) з урахуванням граничних умов дає функцію напружень
В рамках даного наближення Оскільки величина мала, другим доданком можна знехтувати і вважати дотичне напруження постійною величиною
Застосуємо теорему про циркуляцію дотичного напруження до кожного контуру (на рис.2 таких контурів два). При цьому на зовнішньому контурі будемо вважати постійну рівною нулю, на контурі 1 будемо вважати її рівною, а на контурі 2, що дорівнює
Вирішуючи отриману систему відносно постійних, знайдемо
Якщо вважати товщини однаковими, формули спрощуються