Графік функції, що диференціюється називається опуклим вниз (вгору) на інтервалі, якщо він розташований вище (нижче) будь дотичній функції на цьому інтервалі.
Точка графіка функції, яка відокремлює його частини різної опуклості, називається точкою перегину.
ТЕОРЕМА: Якщо функція у всіх точках інтервалу має негативну (позитивну) другу похідну, то графік функції у цьому інтервалі має опуклість догори (вниз).
Приклад 2. Визначити інтервали опуклості і точки перегину графіка функції
Для знаходження інтервалів опуклості і точок перегину необхідно знайти другу похідну функції:;
Прирівняємо другу похідну до нуля і вирішимо вийшло рівняння:
Отримана точка розділить числову вісь на два інтервали. Визначимо знаки другої похідної на цих інтервалах:;
Так як точка належить графіку і при переході через неї друга похідна змінює свій знак, то - точка перегину графіка функції.
На інтервалі друга похідна приймає негативні значення, значить, графік функції має опуклість вгору. Відповідно на інтервалі графік функції має опуклість вниз.
При х → + ∞, х → - ∞ або поблизу точок розриву 2-го роду графік функції може як завгодно близько наближається до будь-якої прямої. Такі прямі називаються асимптотами.
Пряма називається вертикальною асимптотой графіка функції, якщо хоча б один з односторонніх меж цієї функції в точкеа дорівнює + ∞ або -∞.
Можна помітити, що для знаходження вертикальних асимптот достатньою знайти точки розриву 2-го роду. Якщо функція має точку розриву в точці а. то - вертикальна асимптота.
Похила асимптота графіка функції у = f (х) знаходиться у вигляді у = кх + b. де
.
Зауважимо, що якщо хоча б один з коефіцієнтів до або b буде дорівнює нескінченності, то можна зробити висновок, що похилих асимптот немає.
Якщо до = 0. то вертикальна асимптота запишеться у вигляді у = b. Така пряма називається горизонтальною асимптотой.
Приклад 3. Знайти асимптоти функції
Очевидно, що точка буде точкою розриву другого роду, а значить пряма буде вертикальної асимптотой графіка функції.
Перевіримо, чи буде функція мати похилі асимптоти:
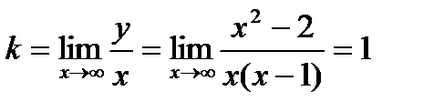
Значить пряма - похила асимптота графіка функції.
Загальна схема дослідження функції
1.Найти область визначення функцій.
2.Найті точки перетину графіка функції з осями координат.
3.Найті екстремуми функції.
4.Найті інтервали монотонності.
5.Найті інтервали опуклості і точки перегину.
7.Найті безліч значень функції
Приклад 4. Дослідити функцію і побудувати її графік
Будемо за загальною схемою досліджувати функцію:
1. Очевидно, що. отже ООФ:
2. Знайдемо точки перетину з осями координат:
. Отримали точки (-; 0); (; 0)
3. Визначимо екстремуми функції:
х = 1 - точка максимуму (1; 2)
х = 3 - точка мінімуму (3; 6)
4. За отриманою вище схемою робимо висновок, що
при функція зростає;
при функція спадає.
Друга похідна приймає позитивні значення при і негативні при. Отже, при графік функції має опуклість вниз, а при графік функції має опуклість вгору.
Точка розділяє частини графіка різної опуклості, але так як ця точка не належить графіку, то точкою перегину вона не є. Інших точок, які поділяють частини графіка різної опуклості немає. Значить, можна зробити висновок, що точок перегину немає.
6. Досліджуємо функцію на асимптоти
Очевидно, що пряма - вертикальна асимптота графіка функції.
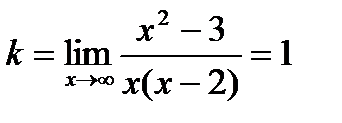
За знайденими точкам побудуємо графік функції, а так же графіки асимптот.
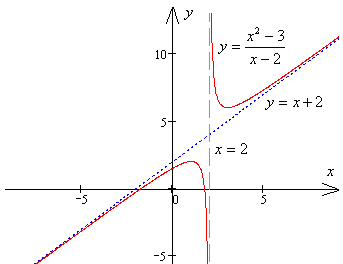
7. За графіком видно, що функція приймає всі значення на числової осі, крім інтервалу від максимуму до мінімуму функції, тобто безліч значень функції:.
Функція F (x) називається первісною функції f (х) на інтервалі, якщо для будь-якого х з цього інтервалу виконується рівність F '(x) = f (х). Безліч всіх первісних функції f (х) задається формулою F (x) + С. Гдесь - постійне число і називається невизначеним інтегралом.
Властивості невизначеного інтеграла:
5) Якщо. то. де - довільна функція, що диференціюється.