Розподіл визначається як дія, зворотне множенню. Приватним двох комплексних чисел z1 і z2 ≠ 0 називається комплексне число z, яке, будучи помноженим на z2. дає число z1. т. е. z1 / z2 = z, якщо z2 z = z1.
Вирішуючи систему, знайдемо значення х і у:
На практиці частка двох комплексних чисел знаходять шляхом множення чисельника і знаменника на число, поєднане знаменника ( «позбуваються від удаваності в знаменнику»).
П.2.5.Ізвлеченіе коренів з комплексних чисел Витяг кореня n-го ступеня визначається як дія, зворотне зведення в натуральну ступінь.
Корнемn-го ступеня з комплексного числа z називається комплексне число ω, яке задовольняє рівності ω n = z, т. Е., Якщо ω n = z.
Якщо покласти z = r (cosφ + isinφ), а ω = r (cosθ + isinθ), то, за визначенням кореня і формулою Муавра, одержуємо
Z = ωn = rn (cos nθ + isin nθ) -r (cosφ + isinφ).
Звідси маємо r n = r, nθ = φ + 2πk, k = 0, -1,1, -2,2. To є
і (арифметичний корінь).
Тому равенствопрінімает вид
Отримаємо n різних значень кореня. При інших значеннях k, в силу періодичності косинуса і синуса, вийдуть значення кореня, що збігаються з уже знайденими. Так, при k = n маємо
Отже, для будь-якого z ≠ 0 корінь n-го ступеня з числа z має рівно n різних значень.
Записати комплексні числа z1 = -1 + i і z2 = -1в тригонометричної і показовою формах.
Рішення: Для z1 маємо
т. е. j = p. Тому -1 = cosπ + isinπ = е iπ.
Рішення: Запишемо спочатку число в тригонометричної формі:
За формулою Муавра маємо
Для тригонометричної форми комплексного числа формула розподілу має вигляд
При розподілі комплексних чисел їх модулі, відповідно, діляться, а аргументи, відповідно, віднімаються.
Рішення: а) Запишемо подкоренное вираз в тригонометричної формі:
.
б) Знову запишемо подкоренное вираз в тригонометричної формі:
-1 = Cosπ + isinπ.
При k = 0 отримуємо ω0 = cos / 2 + isin / 2 = i, а при k = 1 отримуємо
Рішення. Виконуємо дії як над многочленами
Побудувати на комплексній площині і представити в тригонометричної і показовою формах наступні комплексні числа:
1) 2) 3) 4) 5).
Рішення. Спочатку побудуємо всі ці точки на комплексній площині
Тепер уявімо їх у тригонометричної і показовою формах:
Так як 2-ой чверті, то
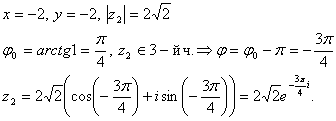
Уявити в показовою формі числа:
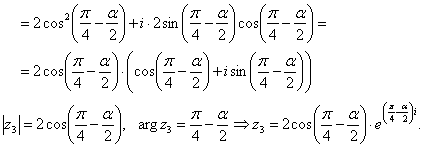
1) Уявімо число в тригонометричної формі
За формулою Муавра отримаємо:
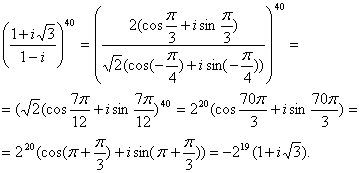
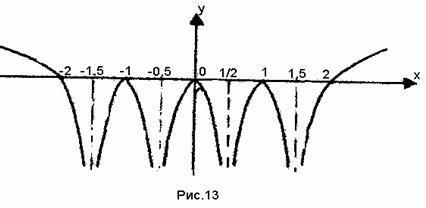
Побудувати графік функції.
Ця функція виду. тобто парна функція і, отже, графік її симетричний щодо осі OY.
Враховуючи що . то слід побудувати графік функцій зрушенням уздовж осі OX на 4 одиниці графіка функції.
1) будуємо графік функції (рис.11);
2) зрушенням його на 4 одиниці по осі OX будуємо графік функції (рис. 11б);
3) зберігаємо праву частину (для) графіка функції і її відображаємо симетрично щодо осі OY. Для уточнення графіка визначимо точку перетину графіка з віссю OY. При. тобто точка перетину графіка з віссю OY: (0; -2). Графік функції представлений на ріс.11в.
Побудувати графік функції.
Так як, то функція парна і графік її симетричний щодо осі OY. Значення x. при яких вираз, що стоїть під знаком логарифма, звертається в нуль, є неприпустимими для x і одночасно вони допомагають знайти вертикальні асимптоти. Знайдемо їх.
.
Графік має чотири вертикальні асимптоти
.
Визначимо нулі функції. маємо:
.
Отже, на осі OX є п'ять точок графіка функції:
(-2; 0), (-1; 0), (0; 0), (1; 0), (2; 0). Графік функції має чотири асимптоти. Для побудови графіка необхідно знати з якого боку гілки графіка наближаються до асимптотам. Для цього досить визначити інтервали знакопостоянства функції. Нагадаємо, що
.
Отже, якщо. то y> 0 і, отже, якщо і. то. Тому графік функції в інтервалі