І
Існує так зване дерево Піфагора - гіпотетичне дерево, яке складено з з'єднаних між собою прямокутних трикутників, з побудованими на катетах і гіпотенузі квадратами.
У теореми Піфагора є наслідок для довільного трикутника:
Сторона трикутника дорівнює кореню квадратному із суми квадратів двох інших її сторін мінус подвоєний добуток цих сторін на косинус кута між ними.
У вигляді формули це записується так:
a 2 = b 2 + c 2 - 2bc * cos α
Це наслідок прийнято називати теоремою косинусів, але по суті - це теорема Піфагора для довільного трикутника.
Існує три формулювання теореми Піфагора:
1. У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів.
2. Площа квадрата, побудованого на гіпотенузі прямокутного трикутника, дорівнює сумі площ квадратів, побудованих на катетах.
3. Квадрат, побудований на гіпотенузі прямокутного трикутника, равносоставлен з квадратами, побудованими на катетах.
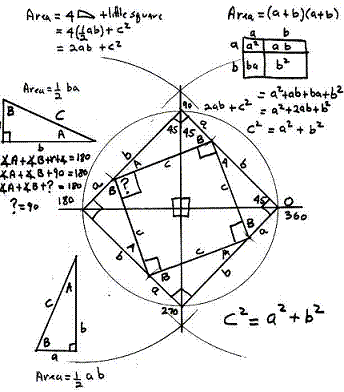
На малюнку зображено два рівних квадрата. Довжина сторін кожного квадрата дорівнює a + b. Кожен з квадратів розбитий на частини, що складаються з квадратів і прямокутних трикутників. Ясно, що якщо від площі квадрата відняти учетверенное площа прямокутного трикутника з катетами a, b, то залишаться рівні площі, т. Е. C2 = a2 + b2. Втім, стародавні індуси, яким належить це міркування, як правило, не записували його, а супроводжували креслення лише одним словом: «дивись!» Цілком можливо, що таке ж доказ запропонував і Піфагор.
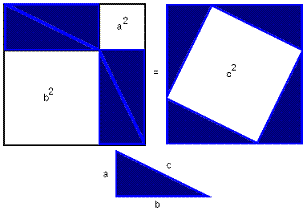
2) Доказ ан-Найрізі *
Доказ ан-Найрізі теж досить легке. Воно примітно тим, що всі фігури збігаються з рівними їм виключно при паралельному перенесенні.
Д
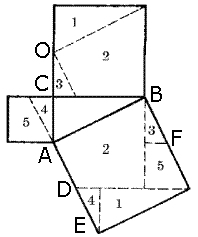
Доведення:
За кресленням ясно видно, що фігруи. відмічені однаковими цифрами, рівні. Трикутники 1 і 1, 3 і 3, 4 і 4 рівні між собою. Чотирикутники 2 і 2, 5 і 5 є рівними. Отже, теорема доведена.
* - латинізоване ім'я - Аннаріцій.
3) Одне з можливих доказів Піфагора
Серед доказів теореми Піфагора алгебраїчним методом перше місце (можливо, найдавніше) займає доказ, що використовує подобу. Наведемо в сучасному викладі одне з таких доказів, можливо належать Піфагору.
Дано: ΔАВС - прямокутний з прямим кутом С; СМ - висота; b1 - проекція катета b на гіпотенузу, а 1 - проекція катета а на гіпотенузу.
Доказ: З того, що ΔABC подібний ΔACM слід:
з того, що ΔABC подібний ΔBCM слід:
Складаючи почленно рівності (1) і (2), отримаємо a 2 + b 2 = cb1 + ca1 = c (b1 + a1) = c 2 .Теорема доведена.
Якщо Піфагор дійсно запропонував такий доказ, то він був знайомий і з цілим рядом важливих геометричних теорем, які сучасні історики математики зазвичай приписують Евклиду.
3) Доказ Гарфілда
Дано: Три пря моугольних трикутника.
Доказ: На ілюстрації три прямокутних трикутника складають трапецію. Тому площа цієї фігури можна знаходити за формулою площі прямокутної трапеції, або як суму площ трьох трикутників. У першому випадку ця площа дорівнює
а в другому випадку
ab / 2 + ab / 2 + c 2/2.
Прирівнюючи ці вирази, отримуємо теорему Піфагора.
4) Доказ засноване на теорії подібності.
У прямокутному трикутника АВС проведемо з вершини прямого кута висоту CD; тоді трикутник розіб'ється на два трикутника, також є прямокутними. Отримані трикутники будуть подібні один одному і вихідного трикутника. Це легко довести, користуючись першою ознакою подібності трикутників (за двома кутами). Справді, відразу видно що, крім прямого кута, трикутники АВС і ACD мають загальний кут a, трикутники CBD і АВС - загальний кут b. Те, що малі трикутники також подібні один одному, випливає з того, що кожен з них подібний до великого трикутника. Втім, це можна встановити і безпосередньо.
Оскільки катети прямокутного трикутника є середнім геометричним між гіпотенузою і проекцією катета на гіпотенузу, маємо:
Складаючи почленно ці рівності, отримуємо:
Теорема знову доведена.
Нікола Леонар Саді Карно (1824)