Центр паралельних сил

Головна | Про нас | Зворотній зв'язок

У цьому розділі розглядаються такі системи паралельних сил, які приводяться до рівнодіючої. Перш за все потрібно відзначити, що умови приведення системи паралельних сил до рівнодіючої зводяться до одного нерівності. Дійсно, вже було показано, що другий інваріант системи паралельних сил тотожно дорівнює нулю. Тому єдиною умовою приведення просторової системи паралельних сил до рівнодіючої є нерівність нулю головного вектора цієї системи

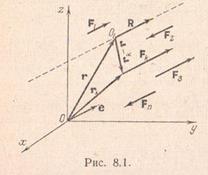
Вважаючи цю умову виконаним, з'ясуємо, що відбувається з рівнодіюча при одночасному повороті раніше напрямів діяльності даних паралельних сил на один і той же кут, якщо точки прикладання цих сил зберігаються незмінними і повороти ліній дії сил відбуваються навколо паралельних осей.

При цих умовах рівнодіюча заданої системи сил також одночасно повертається на той же кут, причому поворот відбувається навколо деякої фіксованої точки, яка називається центром паралельних сил. Перейдемо до доведення цього твердження.

Припустимо, що для даної системи паралельних сил головний вектор не дорівнює нулю, отже, дана система сил приводиться до рівнодіюча. Нехай точка є будь-яка точка лінії дії цієї рівнодіючої. Нехай тепер - радіус-вектор точки відносно обраного полюса. а - радіус-вектор точки прикладання сили.

Згідно з теоремою Варіньона сума моментів всіх сил системи відносно точки дорівнює нулю:

. (8.2) так як точка лежить на лінії дії рівнодіючої.

Отримане рівність можна переписати в такій формі:

Введемо тепер в розгляд одиничний вектор. паралельний лініях дії сил. Тоді будь-яка сила може бути представлена у вигляді

де. якщо напрямок сили і вектора збігаються, і. якщо і спрямовані протилежно один одному. Очевидно, що при цьому

. (8.5) Підставляючи вирази (8.4) і (8.5) в співвідношення (8.3), отримаємо

Остання рівність задовольняється при будь-якому напрямку сил (тобто напрямку одиничного вектора) тільки за умови, що перший множник дорівнює нулю:

У свою чергу це рівність має єдине рішення щодо радіус-вектора. визначального таку точку прикладання рівнодіючої, яка не змінює свого положення при повороті раніше напрямів діяльності сил. Такою точкою і є центр паралельних сил, ніж та доводиться його існування. Позначивши радіус-вектор центра паралельних сил через. з рівності (8.7) отримаємо

Нехай. . - координати центру паралельних сил, а. . - координати точки центру додатки довільної сили; тоді координати точки центру паралельних сил знайдуться з формул:

називаються відповідно статичними моментами заданої системи сил щодо координатних площин. . .

Відзначимо, що якщо початок координат вибрано в центрі паралельних сил, то

і статичні моменти заданої системи сил дорівнюють нулю.

Тіло довільної форми, що знаходиться в полі сил тяжіння, можна розбити перетинами, паралельними координатним площинам, на елементарні обсяги. Якщо знехтувати розмірами тіла в порівнянні з радіусом Землі, то сили тяжіння, що діють на кожен елементарний об'єм, можна вважати паралельними один одному. Позначимо через обсяг елементарного паралелепіпеда з центром в точці. а силу тяжіння, що діє на цей елемент, - через. Тоді середнім питомою вагою елемента обсягу називається відношення. Стягуючи паралелепіпед в точку. отримаємо питому вагу в даній точці тіла, як межа середньої питомої ваги

Таким чином, питома вага є функцією координат, тобто . Будемо вважати, що разом з геометричними характеристиками тіла заданий і питома вага в кожній точці тіла. Повернемося до розбиття тіла на елементарні обсяги. Якщо виключити обсяги тих елементів, які межують з поверхнею тіла, то можна отримати ступеневу тіло, що складається із сукупності паралелепіпедів. Докладемо до центру кожного паралелепіпеда силу тяжіння. де - питома вага в якій частині тіла, що збігається з центром паралелепіпеда. Для системи паралельних сил тяжкості, утвореної таким чином, можна знайти центр паралельних сил

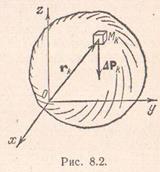
Формула (8.11) визначає положення деякої точки.

Центром тяжіння називається точка, яка є граничною для точок при. Іншим словами, центром тяжіння тіла називається така точка, радіус-вектор якої визначається наступним межею:

(8.12) або, переходячи до питомої ваги,

. (8.13) При такому граничному переході передбачається, що розміри всіх паралелепіпедів прагнуть до нуля. Межі знаменників в формулах (8.12) і (8.13) дорівнюють вазі тіла

Оскільки межі інтегральних сум в чисельнику і знаменнику формули (8.13) являють собою певні інтеграли, поширені за обсягом тіла, то можна представити в наступному вигляді:

Координати центра ваги визначаються формулами:

Тіло називається однорідним, якщо. У цьому випадку величина виноситься в формулах (8.14) за знаки інтегралів в чисельнику і знаменнику і скорочується. Знаменники в формулах (8.14) після скорочення їх на рівні обсягу тіла. Таким чином, отримаємо

Центр тяжкості однорідного тіла часто називають центром тяжіння обсягу.

У ряді випадків тіло можна вважати тонкою пластиною або оболонкою.

Знайдемо центр ваги однорідної оболонки, припускаючи, що вага елемента її поверхні пропорційний площі цього елемента

І, отже, вага тіла (- площа даної частини поверхні).

З визначення центру ваги відповідно до формулами (8.15) отримаємо при

Центр тяжкості однорідної оболонки називають центром тяжіння поверхні.

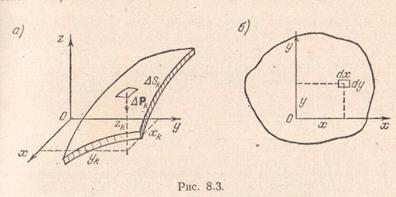
Як випливає з формул (8.16), визначення координат центра ваги поверхні пов'язано з обчисленням інтегралів по поверхні.

Для плоскої однорідної пластини отримаємо

Нарешті розглянемо вигнутий стрижень - тіло подовженої форми, один з характерних розмірів якого значно більше двох інших. Вважаючи, що вага елемента такого стрижня, укладеного між двома перетинами, нормальними до його осі, пропорційний довжині дуги цієї осі, отримаємо

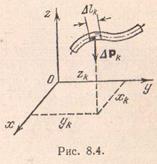
де - довжина стрижня.

Величину називають "погонних вагою". При зробленому припущенні - величина постійна. Тоді відповідно до формулами (8.15) координати центру ваги однорідного стержня мають вигляд

Центр тяжкості криволінійного стержня називають центром тяжіння лінії.

Центр паралельних сил

Схожі статті