Теорія функцій комплексних змінних

Для геометричного зображення комплексного числа z вводять на площині прямокутну декартову систему координат Oxy; вісь Ox називається дійсною, Oy -мнімой осями, а площину Oxy - комплексної площиною (z). Комплексного числа можна поставити у відповідність точку площині (z), або вектор - і крапка і вектор служать геометричному зображенням комплексного числа z -, (рис.1). Модуль вектора називається модулем комплексного числа z; він визначається за формулою

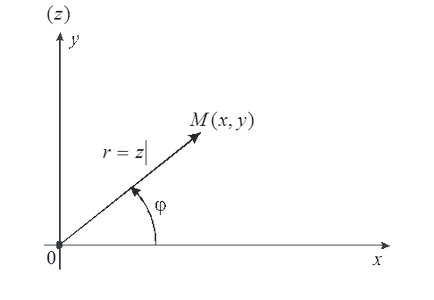
Кут між дійсною віссю Ox і вектором називається аргументом комплексного числа z. . Значення, укладену в проміжку, називається головним значенням аргументу (позначення -arg z):

Головне значення аргументу комплексного числа z можна визначити за формулою

Визначення. запис виду

називається тригонометричної формою записи комплексного числа z.

Зауваження. Комплексне число z записується також у показовій формі

Для порівняння комплексних чисел і вводиться лише операція рівності: комплексні числа і рівні якщо дорівнюють відповідно їх дійсні та уявні частини:. Рівність чисел, записаних в тригонометричної формі, формулюється в такий спосіб:, якщо модулі їх рівні:, а аргументи пов'язані співвідношенням

(Слід звернути увагу на те, що тут порівнювати не елементи множини, а самі нескінченні безлічі).

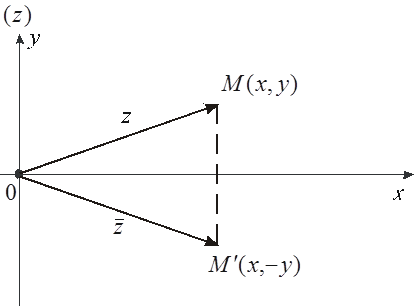
Визначення. Два комплексних числа і називаються комплексно-сполученими числами. Для цього вживають позначення і (рис.2).

16.1.2. Дії додавання, віднімання, множення і ділення.

Дії додавання і віднімання над комплексними числами визначаються геометрично, тобто як відповідні дії над векторами (див. Рис.3) і, отже, виконуються за формулами:

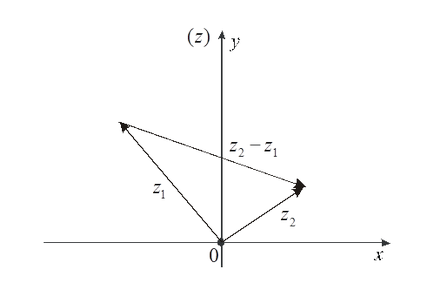
- щоб скласти два комплексних числа (наприклад), потрібно скласти окремо дійсні та уявні частини, що і буде дійсною і уявною частинами суми чисел. З формул (1.7) і (1.8) знаходимо

Під твором комплексних чисел і (позначається) розуміється комплексне число z. рівне

Приватне комплексних чисел і визначається через дію множення і може бути проведено за формулою

Практичні чинять інакше. Так як по формулі (1.10) то розподіл зручно виконувати за наступною формулою:

Так введені операції додавання і множення комплексних чисел підкоряються відомим п'яти законів арифметики:

1. (коммутативность складання);

2. (асоціативність додавання);

3. (коммутативность множення);

4. (асоціативність множення);

5. (дистрибутивность множення щодо

Формула (1.10) "розкриває сенс" уявної одиниці ". Таким чином, множення комплексних чисел здійснюється за звичайними правилами алгебри з заміною на -1.

Наведемо рішення "типових прикладів" на введені вище поняття.

Схожі матеріали