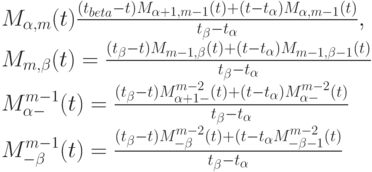Нехай - ціле число. Розглянемо функцію При фіксованому функція розглянута як функція називається усіченою ступеневою функцією.
Лемма 6.1. Для похідних усіченої статечної функції справедливі формули
Позначимо через розділену різницю порядку функції побудовану по вузлах Фіксуємо набір вузлів і розглянемо функцію де розділена різниця обчислюється від розглянутої як функція при фіксованому
Лемма 6.2. Нехай Тоді есліілі
Зауваження 6.1.1. З леми 6.2 випливає, що є безперервною при функцією параметра відмінною від нуля лише на
Приклад 6.1.2. Розділена різниця п'ятого порядку усіченої кубічної функції. Розділена різниця обчислюється від розглянутої як функція при фіксованому Програма демонструє рівність нулю розділеної різниці при всіх лежачих лівіше і правіше всіх вузлів.
На основі розділених різниць ми будемо будувати вагові функції у формулі (6.2) з метою узагальнення раціональних кривих Безьє:
Визначення 6.1.2. Нормованим B-сплайном m-го порядку для неубивающей послідовності вузлів відлічуваної від першого вузла називається функція
Відповідно, ненормованим B-сплайном називається функція
Визначення 6.1.3. Нормованим B-сплайном m-го порядку для неубивающей послідовності вузлів відлічуваної від останнього вузла називається функція
Відповідно визначається і ненормований B-сплайн:
Зауваження 6.1.2. Якщо порядок B -сплайна визначати не числом вузлів мінус одиниця, а ступенем усіченої функції (як многочлена t), то введені вище B -сплайни матимуть (за визначенням) порядок не m. а (m - 1). В цьому випадку для них застосовуються інші позначення: При цьому
І ті й інші позначення присутні в літературі по B -Кривий. Ми будемо користуватися першими. У Mathematica використовуються другі.
Розглянемо (для простоти) нескінченну в обидві сторони послідовність неубутних вузлів де для будь-якого Фіксуємо Тоді визначені безлічі B -сплайнов: сплайни прив'язані до вузла як до першого вузла, сплайни прив'язані до вузла як до останнього вузла
Лемма 6.3. Якщо то серед функцій і тільки m функцій в кожному з цих двох класів можуть бути відмінні від нуля в точці А саме, відмінні від нуля в точці можуть бути лише такі функції:
Лемма 6.4. Для будь-якого має місце
Теорема 6.2 (формула Кокса - де Бура). Справедливі наступні формули для ненормованих B-сплайнів при будь-яких і: