Коли отримана математична модель є складною, тобто нерозв'язною, розробник вдається до її спрощення та використанню більш глибокої абстракції. У практичних завданнях дослідження процесів функціонування складних систем часто бажаний зворотний процес - процес розширення моделі. При цьому починають з побудови простої моделі, а потім ускладнюють її. Еволюційний характер процесу конструювання моделі спрощує рішення поставленого завдання. Спочатку вирішуються більш прості завдання за допомогою простої моделі, а потім ставляться більш складні завдання, що вимагають досягнення більшої відповідності між моделлю і реальним об'єктом, що призводить до ускладнення моделі.
В обох випадках виникає необхідність спрощення математичних моделей об'єкта.
Найбільш поширеними є такі методи спрощення моделей:
1) розчленування складної системи на ряд більш простих підсистем (декомпозиція);
2) виділення істотних властивостей і впливів і облік інших в параметричної формі (метод макромоделювання);
3) линеаризация нелінійних процесів в деякій області зміни змінних;
4) приведення систем з розподіленими параметрами до систем c зосередженими параметрами (введення більш жорстких припущень і обмежень);
5) зневага динамічними властивостями процесів.
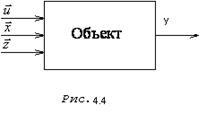
Декомпозиція. У загальному випадку кінцевою метою декомпозиції є розбиття простору змінних об'єкта (рис.4.4.) 1. y2. yn. u1. u2. ur. x1. x2. xm. z1. z2. zl> нa q підпросторів менших розмірностей, в яких враховується тільки зв'язок даного виходу yi з відповідними змінними. Якщо будь-який вихід має зв'язок з іншими виходами, то декомпозиція практично неможлива. Якщо загальна модель об'єкта має вигляд неявного вираження досить великої розмірності
і виходи yi з об'єкта не мають зв'язку між собою, то складну модель (4.33.) можна представити у вигляді сукупності еквівалентних їй n простіших приватних моделей для кожного з виходів
Завдяки проведеній декомпозиції системи значно полегшується завдання її теоретичного дослідження.
Макромоделювання. При використанні методу макромоделювання в вихідному просторі змінних залишаються (тобто враховуються) тільки ті з них, які впливають на вихідні змінні найсильніше. Решта невраховані впливу можуть бути враховані в параметричної формі шляхом зміни коефіцієнтів при врахованих змінних (в разі мультиплікативний впливів) або шляхом введення вільних членів (для адитивних впливів).
При побудові спрощених моделей з урахуванням тільки істотних факторів широко використовується метод адаптивної моделі. тобто моделі, коефіцієнти якої підлаштовуються таким чином, щоб деяка міра розбіжності (невязка) виходів моделі і об'єкта приймала допустимі (мінімальні) значення. Для цього використовують критерії мінімізації нев'язок. Ті змінні, які стабілізуються і не призводять до зміни вихідних змінних, в моделі не відображаються. Структура спрощеної моделі, званої макромоделі, може бути трехканальной з каналом управління u і каналами контрольованих x і неконтрольованих z впливів, двоканальної і одноканальної (рис. 4.5.)
Облік збурень в двоканальних і і в одноканальних моделях проводиться параметрически за рахунок підстроювання коефіцієнтів залишилися каналів.
Повна математична модель
де - вектори контрольованих змінних, причому виконуються умови n1 - вектор параметрів, що коефіцієнтів; - вектори неконтрольованих змінних; Розглянемо як приклад ідею одного з методів адаптації моделей (компенсаційний метод). На рис.4.6: e = (y - yM) - сигнал неузгодженості виходів об'єкта і моделі; АІ - алгоритм ідентифікації. Алгоритм ідентифікації дозволяє налаштовувати модель об'єкта за критерієм мінімуму помилки # 949; шляхом зміни параметрів a1 a2. моделі (ai * оптимальне значення параметра ai). Наведена вище схема працює добре, якщо на її вихід подається сигнал без перешкод. При наявності шуму на вході ставиться завдання придушення перешкод, яку зазвичай вирішують за допомогою диференціальних схем, що містять смугові фільтри (диференційний метод). Лінеаризація. Лінеаризація вихідної нелінійної моделі полегшує вирішення конкретного завдання дослідження. Тому для спрощення моделювання та дослідження, коли це можливо, бажано замінити нелінійне рівняння наближеним лінійним, рішення якого з достатнім ступенем точності описує властивість вихідної нелінійної системи. Процес заміни нелінійної моделі лінійної називається лінеаризацією. Якщо диференціальне рівняння об'єкта нелінійно через нелінійність його статичної характеристики, то для лінеаризації рівняння необхідно замінити нелінійну статичну характеристику y = F (x) лінійною функцією y = a0 + a1 x. Для лінеаризації нелінійної моделі y = F (x) найчастіше застосовують загальноприйнятий метод малих відхилень. Техніка складання лінеаризованих рівнянь принципово проста. Математичне обґрунтування цієї процедури полягає в вимогах до виду нелінійності функції F (x). Для допустимості лінеаризації досить, що F (x) і існують і безперервні в околиці деякої точки (x0. Y0). Тоді линеаризация здійснюється за допомогою розкладання в ряд Тейлора функції F (x, y) в околі точки (x0. Y0) і відкиданням всіх нелінійних членів цього ряду Індекс 0 означає, що похідні беруться в точці x = x0. y = y0. Таким чином, вихідна нелінійна модель замінюється лінійною моделлю виду Такойспособлінеарізаціі означає заміну кривої y = F (x) дотичній в точці (x0. Y0). У разі багатовимірної моделі, тобто моделі виду y = F (x1. X2. Xm) отримаємо В цьому випадку гіперповерхность, описувана нелінійної функцією в просторі змінних x1. x2. xm і y, замінюється гиперплоскостью, дотичній до поверхні в точці (x10. x20. xm0. y0). Інтуїтивно ясно, що лінеаризоване модель, отримана за допомогою розкладання в ряд Тейлора, може виявитися придатною для опису процесів в нелінійній об'єкті, не пов'язаних з великими змінами змінних в околі точки. Помилка моделювання тим менше, чим менше відхилення змінних. Розглянемо процес лінеаризації нелінійної моделі за допомогою розкладання в ряд Тейлора на прикладі об'єкта, поведінка якого описується нелінійним диференціальним рівнянням загального вигляду F (y ", y ', y, x) = 0. (4.39) Якщо x0. y0 - деякий сталий стан, то координати x і y можна записати у вигляді x = x0 + Dx, y = y0 + Dy, де Dx і Dy - відхилення координат x і y від усталеного стану. Рівняння (4.39) в збільшеннях імеіт вид Розкладемо ліву частину рівняння (4.40) в ряд Тейлора щодо точки усталеного стану (0, 0, y0. X0) і полога Dx, Dy і їх похідні за часом малими, відкинемо всі нелінійні члени цього ряду. При цьому отримуємо рівняння яке є лінійним диференціальним з постійними коефіцієнтами. Лінеаризоване рівняння зазвичай записують в наступному вигляді: Необхідною умовою лінеаризації є розкладність в ряд Тейлора функції F (y ", y ', y, x) в околі точки, відповідної сталому станом. Рівняння (4.41) наближено замінює рівняння (4.39) лише в деякій малій околиці точки (0, 0, y0. X0). Величина цієї околиці залежить від виду функції F (y ", y ', y, x), тобто від величин похідних порядки вище першого в даній точці. У більшості випадків за допомогою линеаризованной моделі (4.41) можна дослідити поведінку об'єкта лише при малих відхиленнях вхідний і вихідний координати. Подання вихідної нелінійної залежності у вигляді суми лінійних членів розкладання в ряд Тейлора передбачає відомим вид цієї залежності. Тільки в цьому випадку можливе виявиться обчислення величин похідних. Для цього необхідна побудова складної нелінійної моделі і докладний виписування формул в загальному вигляді з метою подальшого перетворення, що ускладнює процес ідентифікації і збільшують обсяг обчислювальних робіт. Можлива линеаризация нелінійної функції за допомогою січної площини в багатовимірному просторі, описуваної лінійним рівнянням коефіцієнти якого визначаються методом найменших квадратів (МНК) так, щоб отримати хороше наближення вихідної і линеаризованной моделі в деякій області можливих змін змінних. Застосування МНК до обчислення коефіцієнтів лінеаризації істотно впливає на процедуру складання лінійних рівнянь. При такому підході досить задатися структурою лінеаризованого рівняння, тобто вказати склад змінних, від яких повинна залежати досліджувана величина. Звідси легко вбачається перевага застосування МНК для цілей лінеаризації: далеко не завжди можна дати точний вид функціонального зв'язку між змінними в нелінійному вигляді. Для статистичного підходу цього не потрібно, достатньо знати навіть не всі, а лише в основному визначають змінні для опису властивостей реального об'єкта. Це дозволяє відмовитися від процедури побудови нелінійних рівнянь з подальшим їх перетворенням, так як можна відразу ж відшукувати лінійну зв'язок між необхідними за умовою задачі змінними об'єкта. На малюнку 4.7 показана геометрична розглянутих способів лінеаризації, де прийняті наступні позначення: a1 - кут нахилу січної на інтервалі # 8710; Dg (лінеаризація МНК); a2 - кут нахилу дотичної в точці x = 0 (лінеаризація розкладанням в ряд Тейлора). З рис. 4.7 добре видно, що при використанні МНК виявляється можливість дати оцінку допустимого діапазону лінеаризації. Основою для цього служить властивість МНК визначати найкращі значення шуканих коефіцієнтів лінійної моделі в прийнятому діапазоні. 4. Спрощення моделі з розподіленими параметрами. Характеристики стану об'єкта можуть залежати не тільки від часу, але і від просторових координат. З безлічі об'єктів з розподіленими параметрами можна виділити об'єкти, параметри яких приводили до зосередженим. Це такі об'єкти, для яких досить знати значення вхідних і вихідних змінних в кінцевому числі фіксованих точок простору. Наприклад, лінійні об'єкти з розподіленими параметрами структурно можуть бути представлені у вигляді багатовимірного лінійного об'єкта з зосередженими параметрами. Тоді процеси в таких об'єктах будуть описані сукупністю математичних моделей, що визначають зміни тільки в часі досліджуваних вихідних величин об'єктів в кожній фіксованій точці простору.Схожі статті