Визначення функції Ляпунова
Функція Ляпунова являє собою скалярную функцію, задану на фазовому просторі системи, за допомогою якої можна довести стійкість положення рівноваги. Метод функцій Ляпунова застосовується для дослідження стійкості різних диференціальних рівнянь і систем. Нижче ми обмежимося розглядом автономних систем \ [= \ mathbf \ left (\ mathbf \ right) \; \; \ text> \; \; >>> = \ left (,, \ ldots,> \ right),> \; \; \] Мають нульове положення рівноваги \ (\ mathbf \ equiv \ mathbf. \)
Припустимо, що в деякій околиці \ (U \) початку координат задана безперервно диференціюється функція \ [V \ left (\ mathbf \ right) = V \ left (,, \ ldots,> \ right). \] Нехай \ (V \ left (\ mathbf \ right)> 0 \) для всіх \ (\ mathbf \ in U \ backslash \ left \<\mathbf \right\>,\) А на початку координат \ (V \ left (\ mathbf \ right) = 0. \) Такими функціями є, наприклад, функції виду \ [,> \ right) = ax_1 ^ 2 + bx_2 ^ 2,> \; \ ; ,> \ Right) = ax_1 ^ 2 + bx_2 ^ 4,> \; \; 0.> \] Знайдемо повну похідну функції \ (V \ left (\ mathbf \ right) \) за часом \ (t: \) \ [>> = \ frac >>> \ frac >>> + \ frac >> > \ frac >>> + \ cdots> + >>> \ frac >>>.> \] Цей вислів можна записати у вигляді скалярного добутку двох векторів: \ [>> = \ left (\, V, \ frac >> >> \ right), \; \; \ text \; \; >>>>, \ frac >>>, \ ldots, \ frac >>>> \ right),> \; \; >>> = \ left (>>>, \ frac >>>, \ ldots, \ frac >>>> \ right).> \] Тут перший вектор являє собою градієнт функції \ (V \ left (\ mathbf \ right), \) т . Е. він завжди спрямований у бік найбільшого зростання функції \ (V \ left (\ mathbf \ right). \) Як правило, функція \ (V \ left (\ mathbf \ right) \) зростає при видаленні від початку координат, тобто за умови \ (\ left | \ mathbf \ right | \ to \ infty. \) Другий вектор в скалярному творі - це вектор швидкості руху. У будь-якій точці він спрямований по дотичній до фазової траєкторії.
Розглянемо випадок, коли похідна функції \ (V \ left (\ mathbf \ right) \) в околиці \ (U \) початку координат негативна: \ [\ frac >> = \ left (\, V, \ frac >>>> \ right) 0 \) для всіх \ (\ mathbf \ in U \ backslash \ left \<\mathbf \right\>\);
\ (V \ left (\ mathbf \ right) = 0 \);
Теореми про стійкість
Теорема про стійкість в сенсі Ляпунова. Якщо в деякому околі \ (U \) нульового рішення \ (\ mathbf = \ mathbf \) автономної системи існує функція Ляпунова \ (V \ left (\ mathbf \ right), \) то положення рівноваги \ (\ mathbf = \ mathbf \ ) є стійким по Ляпунову.
Теорема про асимптотичну стійкість. Якщо в деякому околі \ (U \) нульового рішення \ (\ mathbf = \ mathbf \) автономної системи існує функція Ляпунова \ (V \ left (\ mathbf \ right) \) з негативно певної похідною \ (>> \ normalsize> 0 \).
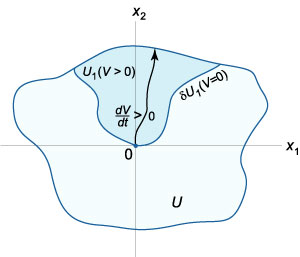
Якщо в околиці \ (U \) є точки, в яких \ (V \ left (\ mathbf \ right)> 0, \) то нульовий розв'язок \ (\ mathbf = \ mathbf \) є нестійким. Теорема Четаева про нестійкість. Нехай в околиці \ (U \) нульового рішення \ (\ mathbf = \ mathbf \) автономної системи існує безперервно диференціюється функція \ (V \ left (\ mathbf \ right). \) Нехай околиця \ (U \) містить подобласть \ ( , \) включає початок координат (рис. \ (3 \)), таку, що
\ (V \ left (\ mathbf \ right)> 0 \) для всіх \ (\ mathbf \ in \ backslash \ left \<\mathbf \right\>\);
\ (V \ left (\ mathbf \ right) = 0 \) для всіх \ (\ mathbf \ in \ delta, \) де \ (\ delta \) позначає кордон подобласти \ (\).
Тоді нульове рішення \ (\ mathbf = \ mathbf \) системи нестійка. В цьому випадку фазові траєкторії в підобласті \ (\) будуть прагнути від початку координат.
Таким чином, функції Ляпунова дозволяють встановити стійкість або нестійкість системи. Перевагою даного методу є те, що тут не потрібно знати саме рішення \ (\ mathbf \ left (t \ right). \) Крім того, даний метод дозволяє досліджувати стійкість положень рівноваги не грубих систем, - наприклад, у разі, коли точка рівноваги є центром. Недолік полягає в тому, що не існує загального методу побудови функцій Ляпунова. В окремому випадку однорідних автономних систем з постійними коефіцієнтами функцію Ляпунова можна шукати у вигляді квадратичної форми.