Алгебри різного типу, очевидно, мають істотно різну будову. Якщо ж алгебри мають однаковий тип, то наявність у них подібності характеризується за допомогою вводяться нижче понять гомоморфизма і ізоморфізму.
Нехай дано дві алгебри
однакового типу, т. е. арності і; і; і - однакові.
Гомоморфизмом алгебри А в алгебру В називається відображення -. задовольняє умові:
для всіх (- арность операцій і.
Сенс умови (1):
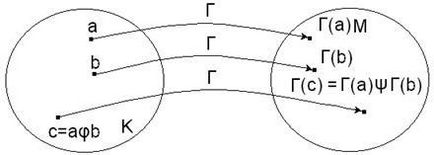
незалежно від того, чи виконана спочатку операція в безлічі K і потім вироблено відображення Г, або спочатку вироблено відображення Г, а потім в множині M виконана відповідна операція. результат буде однаковий.
Изоморфизмом алгебри А на алгебру В називається взаємно однозначну гомоморфізм. У цьому випадку існує зворотне відображення. так само взаємно однозначне.
Нехай. . Тоді. Замінимо в (1) ліві частини цих рівностей на праві і застосуємо до обох частин отриманого рівності. Так як . то отримаємо:
Рівність (2) - це той же рівність (1) з заміною Г на. елементів безлічі K на елементи безлічі М і зміною місцями і. Інакше кажучи, - це ізоморфізм В на А.
Якщо існує ізоморфізм А на В. то існує ізоморфізм В на А; при цьому алгебри А і В називаються ізоморфними.
Потужності несучих множин ізоморфних алгебр рівні (при гомоморфізм це рівність може не виконуватися).
Автоморфізм на себяіліавтоморфізм - це гомоморфізм за умови, що А = В.
Ізоморфізм в себе - ізоморфізм.
1. Нехай - множина всіх цілих чисел; - безліч всіх парних чисел;
а) алгебри і ізоморфні. Изоморфизмом є відображення. причому, умова (1) тут має вигляд: 2 (a + b) = 2a + 2b. Оскільки. то Г - ізоморфізм алгебри в себе.
б) відображення є для алгебри автоморфизмом.
Умова (1) має вигляд:
в) відображення для алгебри не є автоморфизмом, так як
2. ізоморфізм між алгебра і є відображення (- позитивне підмножина R).
Умова (1) має вигляд рівності:
3. Булеві алгебри Кантора B (U),) і B (),), утворені двома різними множинами U і однакової потужності, ізоморфні. Операції у них просто однакові, а відображенням Г може служити будь-який взаємно однозначна відповідність між U і.
Ставлення ізоморфізму є відношенням еквівалентності на безлічі алгебр:
- рефлексивність відносини ізоморфізму очевидна;
- симетричність випливає з існування зворотного ізоморфізму;
- транзитивність встановлюється наступним чином: якщо - ізоморфізм А на В. - ізоморфізм В на С. то изоморфизмом А на С буде композиція і.
Класами еквівалентності в розбитті по відношенню ізоморфізму є класи ізоморфних між собою алгебр. Поняття ізоморфізму - одне з найважливіших в математиці. Його сутність, як видно з прикладів можна висловити так: якщо алгебри А і В ізоморфні, то елементи і операції в В можна перейменувати так, що В співпаде з А.
З умови (1) ізоморфізму слід, що будь-який еквівалентний співвідношення в алгебрі А зберігається в будь-який изоморфной їй алгебри. Це дозволяє отримати такі співвідношення в алгебрі А і автоматично поширити їх на всі алгебри, ізоморфні А. Поширена в математиці вираз «розглядати з точністю до ізоморфізму» означає, що розглядаються тільки ті властивості об'єктів, які зберігаються при ізоморфізмі, т. Е. Є загальними для всіх ізоморфних об'єктів.
Зокрема, ізоморфізм зберігає асоціативність, комутативність, дистрибутивность.