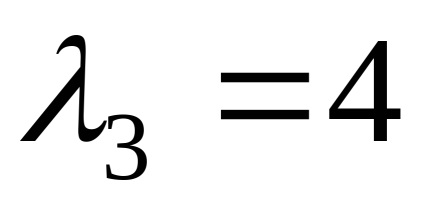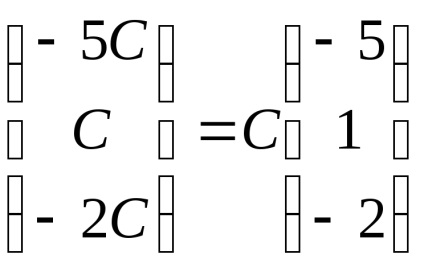Вирішивши останнє рівняння щодо



Розглянемо кілька прикладів, в кожному з яких будемо виконувати послідовність дій рішення задачі про відшукання власних значень і власних векторів матриці.
Знайти власні значення і власні вектори матриці
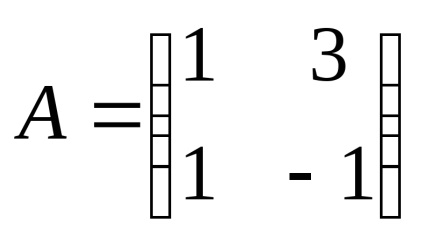
Матриця має розмірність 2

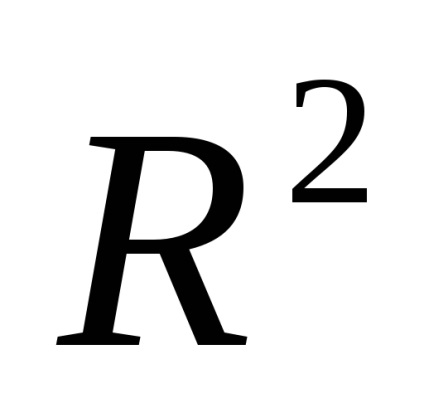
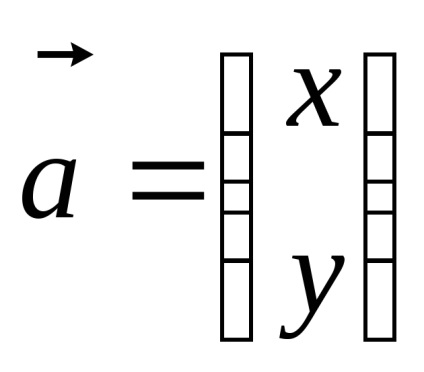
Складемо рівняння для відшукання власних векторів в матричному вигляді:
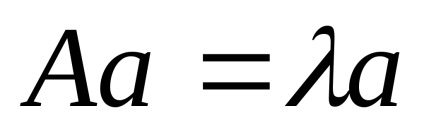

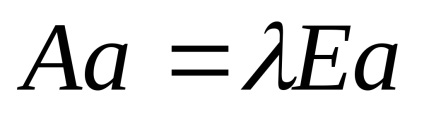

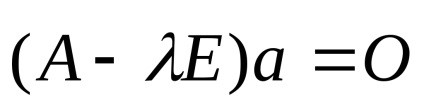
3. Перепишемо матричне рівняння у вигляді системи рівнянь:
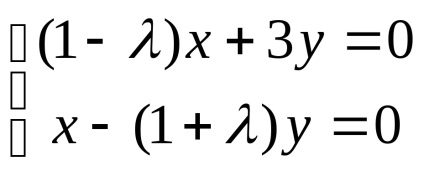
Однорідна система має ненульові рішення тоді і тільки тоді, коли визначник її головною матриці дорівнює 0. Отримуємо характеристичне рівняння системи і вирішуємо його:
.
Власні значення матриці

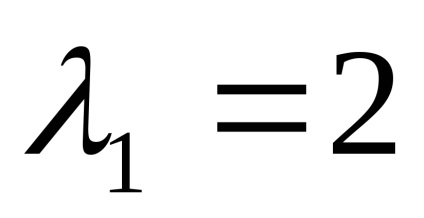
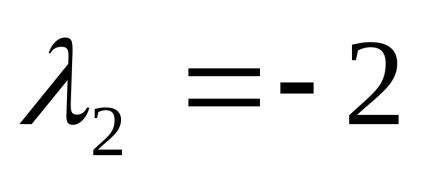
Знайдемо власні вектори для кожного власного значення:
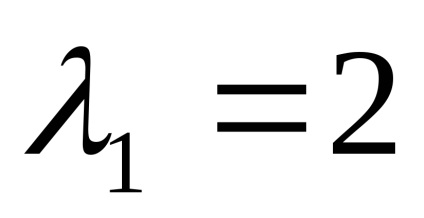
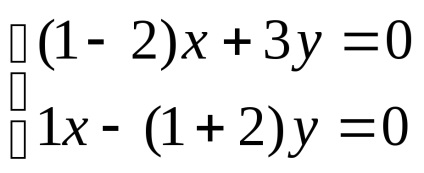
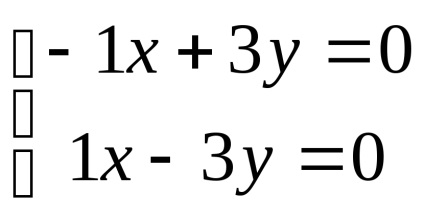
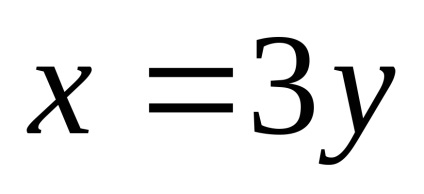
нехай
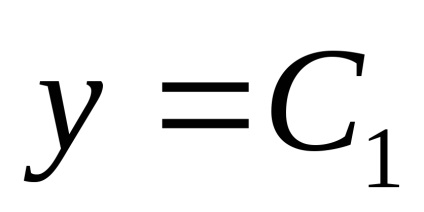

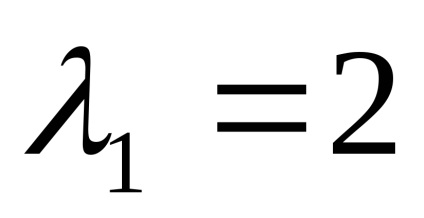
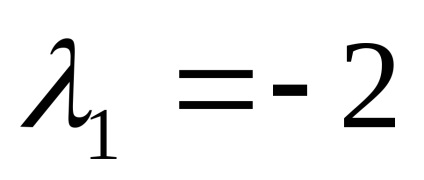
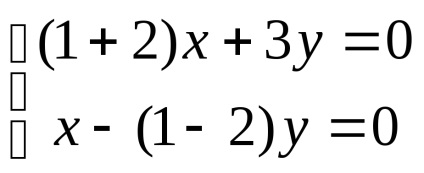
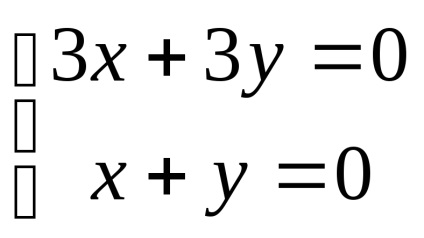
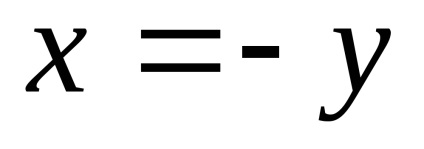
нехай
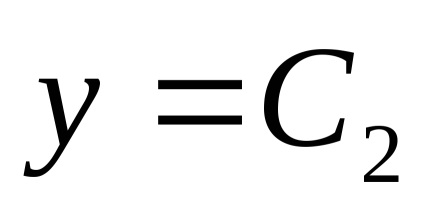

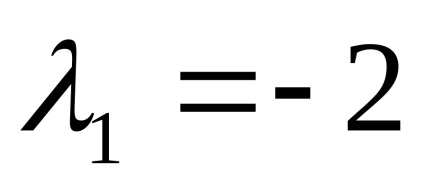
Приклад 2. Знайти власні значення і власні вектори лінійного оператора. заданого в деякому базисі матріцейА =
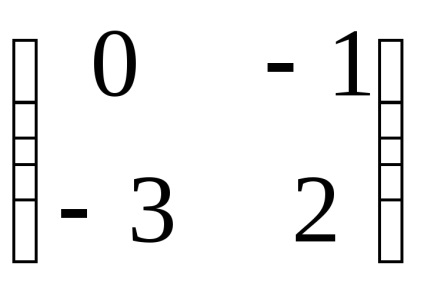
Складемо і вирішимо характеристичне рівняння
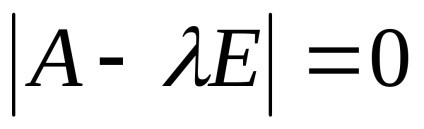
Тоді характеристичне рівняння приймає вид:
,
,
- власні значення лінійного оператора.
Знайдемо власні вектори, відповідні власним значенням
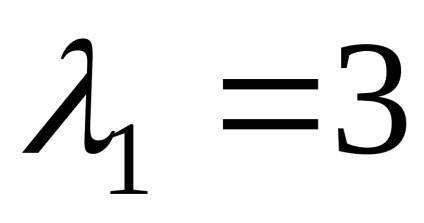
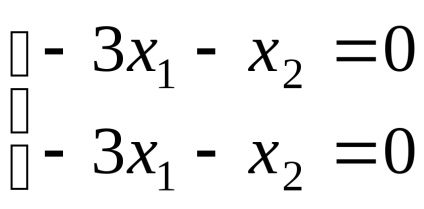
Вважаючи в останній рівності
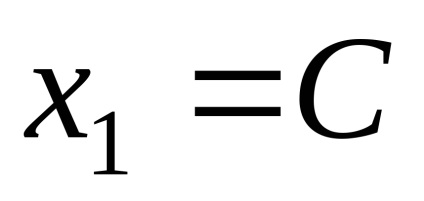
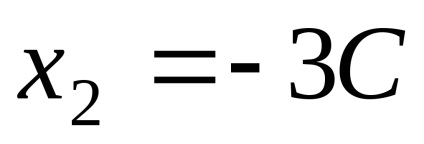
Звідки власні вектори, відповідні власним значенням
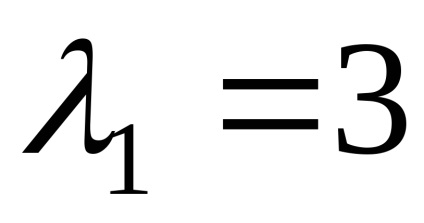
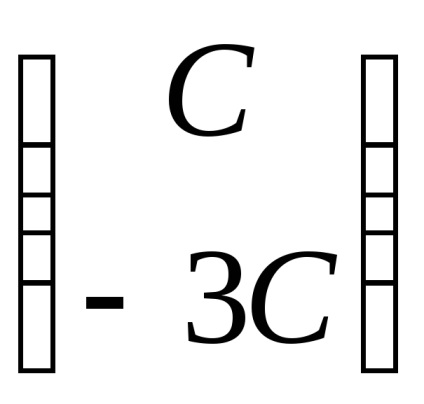
Знайдемо власні вектори, відповідні власним значенням
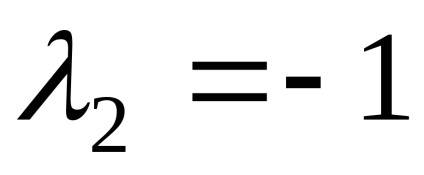
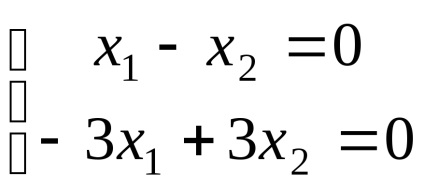
Вважаючи в останній рівності
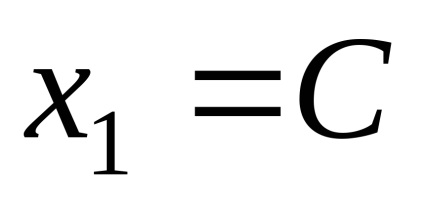
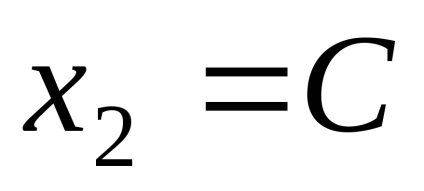
Звідки власні вектори, відповідні власним значенням
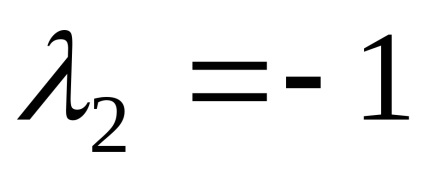
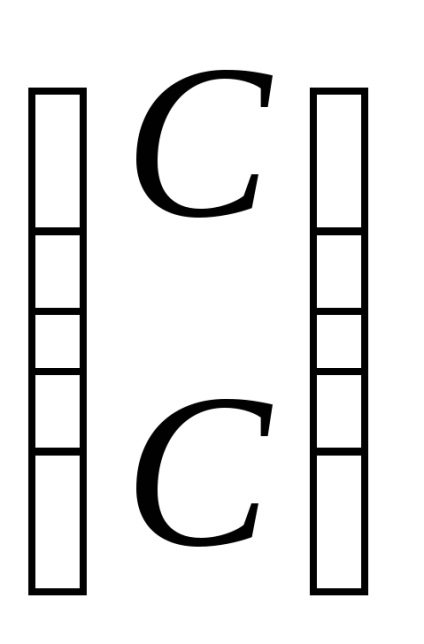
Відповідь. своїм значенням
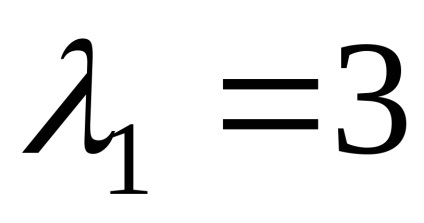
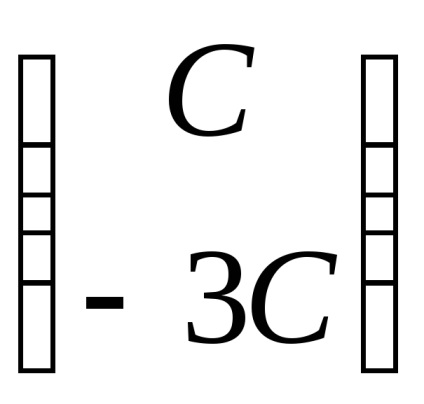
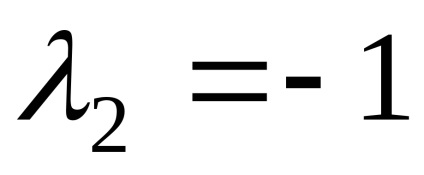
Приклад 3. Знайти власні значення і власні вектори лінійного оператора. заданого в деякому базисі матріцейА =
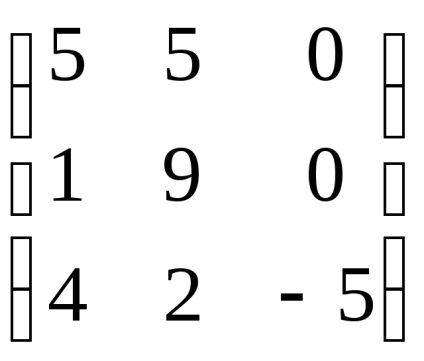
Знайдемо власні значення лінійного оператора. Для цього складемо характеристичне рівняння і знайдемо його корені:
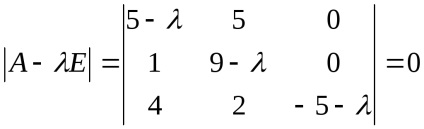
,
,
,
,
, ,
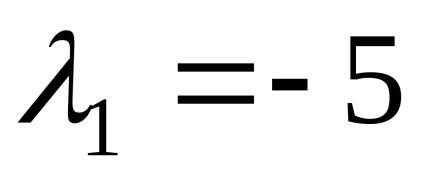
Знайдемо власні вектори, відповідні власним значенням
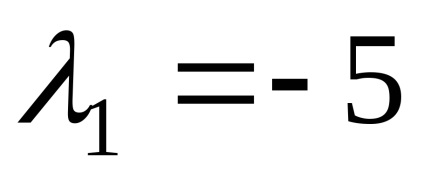
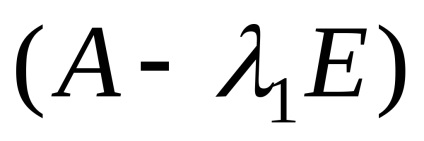
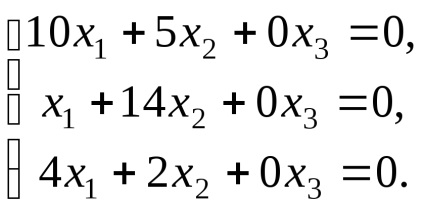

Оскільки ранг матриці системи (r = 2) менше кількості невідомих, то система має безліч рішень. Записуючи перетворену систему і вирішуючи її, отримаємо,
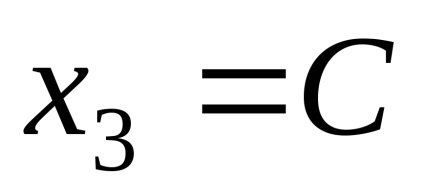
Таким чином, власні вектори, відповідні власним значенням
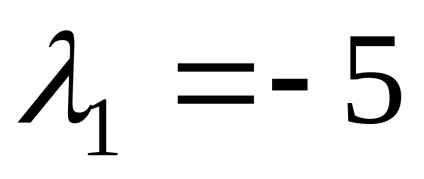
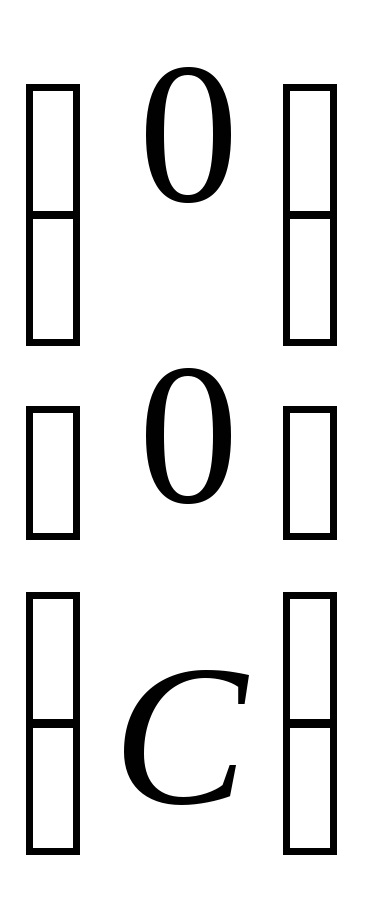
Знайдемо власні вектори, відповідні власним значенням
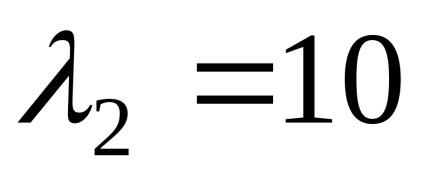
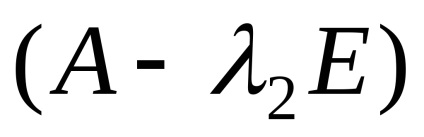
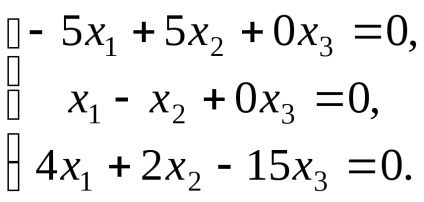
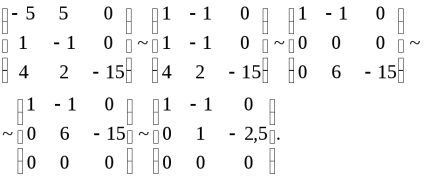
звідки, система приймає вигляд
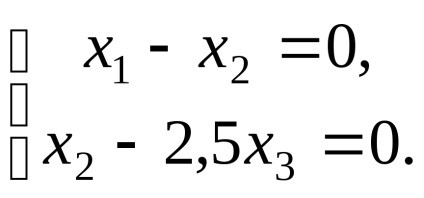
Таким чином, власні вектори, відповідні власним значенням
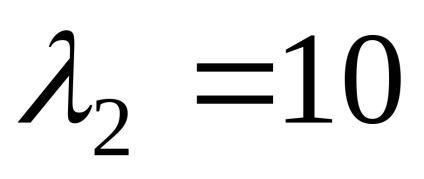
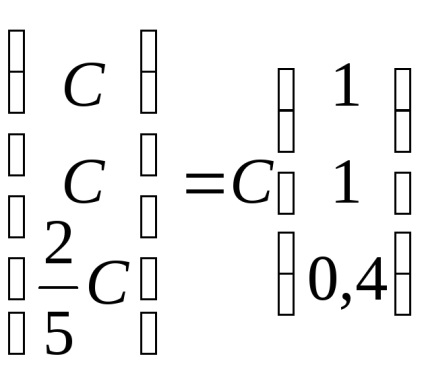
Знайдемо власні вектори, відповідні власним значенням
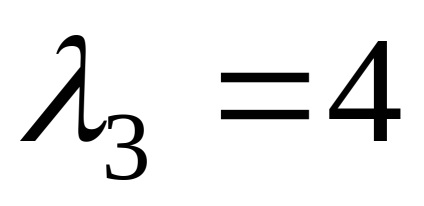
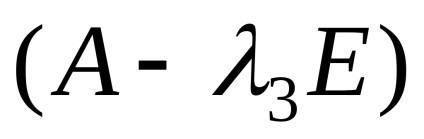
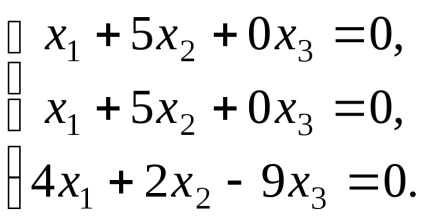
,
звідки, система приймає вигляд
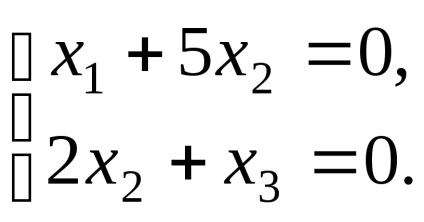
Таким чином, власні вектори, відповідні власним значенням