Позначимо. .
Тоді і називаються відповідно нижньою і верхньою сумами Дарбу.
Цей загальний межа сум Дарбу і є межа інтегральної суми, що дорівнює за визначенням певного інтеграла.
= = =.
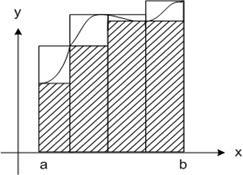
Геометрично суми Дарбу є площі східчастих фігур, які є наближеннями площі криволінійної трапеції, обмеженою графіком функції і прямими. Причому нижня сума - наближення з недоліком, а верхня - з надлишком. Таким чином, певний інтеграл від неотрицательной функції є площа криволінійної трапеції.
Для того, щоб функція була інтегрована на відрізку. її безперервність на цьому відрізку не обов'язкова. Достатньою умовою інтегрованості функції на відрізку є її кусково безперервність на цьому відрізку.
Функція називається кусочно безперервної на відрізку якщо вона має на цьому відрізку кінцеве число точок розриву першого роду.
Приклад. Обчислити площу фігури, обмеженою параболою і прямими.
Рішення. Розіб'ємо проміжок інтегрування на рівних частин довжиною. - точки ділення. Беручи до уваги те, що функція строго зростає на проміжку. складемо суми Дарбу, і знайдемо їх межі прі.
= =. .
= =.
.
Так як - площа ступінчастою фігури, менша шуканої площі, а
- площа ступінчастою фігури, велика шуканої площі, то шукана площа
= =.
Межі нижньої і верхньої сум Дарбу збігаються, отже, функція інтегровна на проміжку і
.
Приклад. За допомогою певного інтеграла знайти межу суми
.
Рішення. Уявімо шукану суму у вигляді інтегральної суми =. У цій сумі. Але тоді
= (Згідно попереднього прикладу).
Рішення. Покладемо Тоді права частина тотожності дорівнює
Неважко помітити, що ліву частину тотожності можна уявити в такому ж вигляді. Залишилося показати, що існує кінцевий межа цього виразу
при
=.
Отриманий вираз є інтегральною сумою, отже,