Комсомольська ЗОШ №5 І - ІІІ ступенів
РІШЕННЯ РІВНЯНЬ, ЩО МІСТЯТЬ ЗНАК МОДУЛЯ
Рішення рівнянь з модулем викликає в учнів труднощі.
Аналізуючи завдання вступних іспитів, необхідно відзначити, що дуже часто пропонуються завдання з модулями. Щоб допомогти учням навчитися розв'язувати рівняння з модулями пропонується даний матеріал.
Рівняння з модулем розділені на групи за способом їх вирішення. До кожної групи дається теоретичний матеріал. необхідний для вирішення рівнянь даної групи.
Дано рішення рівнянь кожної групи, а до окремих рівнянь алгоритм їх вирішення, що дозволяє учням самообучаться.
Цей матеріал можна застосовувати на уроках при роботі по групах і індивідуально як в класі, так і для домашньої роботи.
Призначається учням стерши класів.
Містять змінну ПІД ЗНАКОМ МОДУЛЯ
Найпростішими рівняннями з модулем є рівняння виду, (1)
де і - деякі функції.
Для того щоб вирішити дане рівняння, потрібно знайти спочатку всі рішення рівняння =, що належать безлічі, потім вирішити рівняння = на безлічі; об'єднання множин знайдених рішень становить безліч всіх рішень рівняння (1). Іншими словами, рівняння (1) рівносильне сукупності систем
Початкове рівняння рівносильне сукупності систем:
Відповідь. - 3; - 2; 2; 3.
Рівняння виду рівносильно сукупності систем (можна вирішити двома способами)
Дане рівняння рівносильне сукупності систем:
не задовольняє умові, отже, система має рішення.
не задовольняє умові, отже, друга система має рішення.
Рівняння виду, де - деякі функції, рівносильно сукупності систем
Дане рівняння рівносильне сукупності двох систем:
1). система не має рішень.
При вирішенні рівняння, в якому під знаком модуля знаходиться вираз, що містить модуль, слід спочатку звільнитися від внутрішніх модулів, а потім в отриманих рівняннях розкрити залишилися модулі.
Дане рівняння рівносильне сукупності двох систем
тобто сукупності систем
Друга система рішень не має. Перша система рівносильна двом наступним системам:
5. Метод розбиття на проміжки. Рівняння виду (2)
Вирішується методом інтервалів (або методом розбиття на проміжки). Для цього знаходять спочатку всі крапки, в яких
Ці точки ділять область допустимих значень рівняння (2) на проміжки, на кожному з яких всі функції зберігають знак (вважаємо знак кожного модуля на зазначеному проміжку). Потім переходять від рівняння (2) і сукупності систем, що не містять знаків модуля.
18. Знайдіть всі коріння рівняння, що задовольняють нерівності.
ВІДПОВІДІ І РІШЕННЯ.
2. Скористайтеся методом розбиття на проміжки.
З модулів, що містять ПАРАМЕТР.
1. Для кожного значення параметра знайдіть число коренів рівняння.
Рішення. Запишемо рівняння у вигляді, так як не є коренем рівняння. Кількість коренів даного рівняння буде відповідати кількості точок перетину графіка функції з прямою. Побудуємо графік функції, який складається з двох частин:
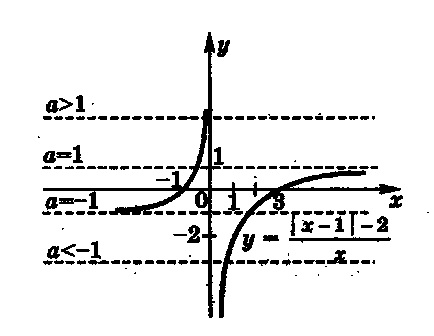
З малюнка видно, що
при має єдину точку перетину, а значить, єдиний корінь;
при має дві точки перетину, а значить, вихідне рівняння має два кореня;
при - одна точка перетину, а значить, рівняння має єдиний корінь.
Залишилося перевірити, скільки коренів має вихідне рівняння при і.
Нехай, тоді вихідне рівняння прийме вид. Визначимо кількість коренів даного рівняння.
Нехай, тоді маємо рівняння:
Відповідь: при рівняння має єдиний корінь;
при рівняння має два кореня;
при рівняння має єдине рішення.
2. Для кожного значення параметра знайдіть число коренів рівняння.
Рішення. Перепишемо рівняння у вигляді.
Для вирішення завдання визначимо кількість точок перетину графіка функції і. Побудуємо графік функції
який складається з двох частин:
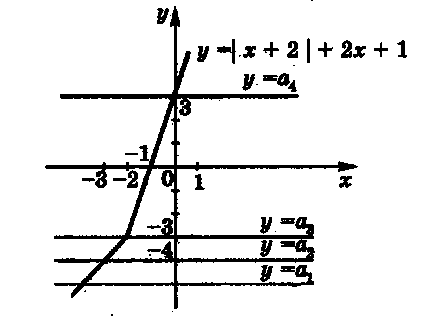
З малюнка видно, що при будь-якому значенні параметра вихідне рівняння має один корінь.
Відповідь: при будь-якому значенні параметра вихідне рівняння має один корінь.
3. При яких значеннях параметра рівняння
Має хоча б одне рішення?
Рішення. підмодульних функція
Якщо, то, так як, причому рівність досягається тільки при, тобто.
Якщо, то, рівність досягається тільки при.
Отже, при всіх. Так як, то рівняння (1) рівносильне системі і тільки при знайдених значеннях параметра вихідне рівняння має рішення, а саме.
1. Для кожного значення параметра знайдіть число коренів рівняння
2. Для кожного значення параметра знайдіть число коренів рівняння
3. При яких значеннях параметра рівняння має хоча б одне рішення?
1. При рівняння має єдиний корінь;
при рівняння має два кореня.
2. При будь-якому значенні параметра рівняння має єдиний корінь.