Сьогодні ми поговоримо про таку тему, яка хвилює всіх учнів 8-9 класів, коли вони починають вивчати серйозну дорослу тригонометрію. Йдеться про радіанної міру кута, а також про переведення з радіанної в градусну міру кута і назад. Але, перш ніж ми почнемо вирішувати якісь завдання на обчислення радіанної заходи, мені хотілося б згадати старе визначення, що таке синус, косинус і тангенс кута в прямокутному трикутнику.
трохи теорії
Давайте намалюємо прямокутний трикутник, назвемо його
причому C C буде прямим:
Кут A A буде дорівнює α \ alpha градусів. У цьому випадку, як ви пам'ятаєте зі шкільного курсу геометрії, синус, косинус і тангенс будуть однакові:
Як бачите, класичне визначення синуса, косинуса, тангенса і котангенс зав'язано на прямокутному трикутнику, і α \ alpha в будь-якому випадку повинен бути більше 0º і менше 90º.
Незважаючи на це, виникла необхідність розширити визначення тригонометричних функцій за межі цього інтервалу від 0º до 90º. Як це відбувається, і які виникають при цьому ефекти - ось зараз про це і поговоримо.
Для початку давайте розглянемо координатну площину: проведемо осі x x, y y, а також побудуємо одиничну окружність з центром на початку координат:
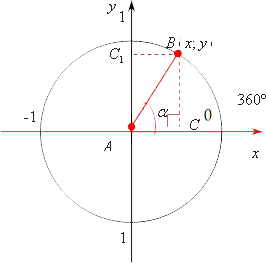
Невелике уточнення в термінології, що означає одиничне коло? Все дуже просто. Це означає, що її радіус дорівнює строго 1. Іншими словами, вона проходить через точку (1; 0), а також (0; 1). І через дві інші точки ця окружність також проходить. Тепер нам потрібно пустити від початку координат промінь уздовж осі Ox Ox. Йдеться про позитивному напрямку осі Ox Ox. Потім ми відзначимо α \ alpha в напрямку x x до y y. Зрозуміло, цей промінь перетне наш коло в якомусь значенні, давайте позначимо його точкою B B. А початок координат позначимо точкою A A. Проведемо з B B висоту до осі абсцис x x. Ми отримаємо C C. Ось ми знову отримали той же самий прямокутний трикутник ABC ABC з кутом α \ alpha. вершина якого збігається з початком координат.
Що таке синус?
Тепер давайте перепишемо синус, косинус і тангенс з урахуванням всіх змін для червоного трикутника. запишемо:
Все теж саме. Однак зауважимо, що B B лежить вже не в якомусь невизначеному просторі, вона має якісь координати, оскільки лежить в площині Oxy Oxy. Нехай її координати будуть (x; y) \ left (x; y \ right). Ми не знаємо точно, чому вони рівні, бо не знаємо кут α \ alpha. У такому випадку довжина відрізка BC BCравняется yy, т. Е. Ординате точки B B. Замість BC BC ми можемо записати yy, а замість AB AB - 1. AB AB - це той же самий радіус нашого кола, а радіус - 1. Записуємо :
sinα = BC AB = y r = y
Таким чином, ми можемо записати, що sinα \ sin \ alpha насправді дорівнює ординате кінця рухомого радіуса. Ось саме цю фразу найчастіше зустрічають учні в шкільних підручниках з математики. Тому, перш ніж рушимо далі, давайте ще раз уважно подивимося на трикутник ABC ABC і, зокрема, на B B.
Ми провели ще одну висоту, назвемо її B C 1 B_>. Що можна сказати про C 1 _>, точніше, про відрізок AC 1 A_> - це координата у B B. З іншого боку, відрізок AC AC, т. Е. Відстань від AA до CC - це координата xx точки CC і, відповідно , xx точки B B. Нам нескладно буде довести, що відрізки BC BC і AC 1 A_> рівні. Тоді ми можемо стверджувати, що і відрізок AB AB теж дорівнює y y. Таким чином, з синусом ми розібралися. Дійсно, синус кута α \ alpha дорівнює ординате кінця рухомого радіуса, проведеного в точку B B. Тепер давайте запишемо ті ж самі вирази для косинуса і тангенса.
Що таке косинус?
Це відношення прилеглого катета (в нашому випадку це катет AC AC) до гіпотенузи (у нас AB AB). Але що таке AC AC? Тільки що ми переконалися, що AC AC - це абсциса, т. Е. Координата x x. А AB AB - це той же самий радіус, т. Е. 1. Запишемо:
cosα = AC AB = x r = x
Що таке тангенс?
Тепер розбираємося з tg α tg \ alpha. Тут все ще простіше. Що таке тангенс? Це відношення протилежного катета (а нашому випадку це BC BC) до прилеглого катета (в нашому випадку це AC AC). запишемо:
tg α = BC AC = y x
Таким чином, tg tg - це відношення ординати до абсциссе кінця рухомого радіуса.
І в цей момент багато учнів напевно спитають: «А навіщо взагалі вся ця складність?». В даному випадку коли B B просто задається перетином променя з окружністю, ми можемо відкласти будь-який кут α \ alpha. Тепер ніяких обмежень на позначення α \ alpha не накладаються. Він не зобов'язаний бути кутом межах від 0º до 90º.
Обчислення радіанної міри кута
Тепер, коли ми розібралися з основними визначеннями тригонометричних функцій, перейдемо безпосередньо до сьогоднішньої теми уроку.
Для початку давайте розглянемо кут в 180º. Тоді наш промінь підчепити в протилежному напрямку. Точка В в нашому трикутнику висікає певну дугу окружності. Назвемо її дуга BC BC. Її легко порахувати за формулою довжини кола:
\ Pi \ tilde3,14. Але зараз нас це не цікавить. Оскільки наша окружність завжди має фіксований радіус 1, то довжина дорівнюватиме:
Однак 2π 2 \ pi - це вся окружність, т. Е. Повний оборот. А ми якщо відступимо на 180º, то отримаємо тільки її половину. Отже, дуга окружності дорівнюватиме:
l (180 o) = 2π 2 = π
l \ left (180<>^ \ Text \ right) = \ frac = \ pi
І ось тут виникає чудовий ефект. Справа в тому, що один і той же кут α \ alpha ми можемо позначати як за 180º, т. Е. Використовувати стандартну міру кута (а не Радіан), так і довгою ось цієї дуги, т. Е. Ми можемо поставити кутку α \ alpha відповідне число π \ pi. Так ось це число π \ pi. т. е. іншими словами, кут, виміряний не в градусах, а в довжині дуги, яку цей кут висікає. Називається це Радіанна міра кута і позначається π \ pi - радіан.
Сьогодні ж для того щоб почати вирішувати завдання на Радіан міру і вважати значення тригонометричних функцій, просто запам'ятайте, що π \ pi рад = 180º. Іншими словами, якщо вам незвично працювати з Радіан значеннями, то скрізь, де ви бачите в синусах, косинусів і тангенсів конструкцію π \ pi. ви можете сміливо замінити це π на 180º і перейти до знайомої градусної від радіанної заходи. Давайте спробуємо і порахуємо перший вираз і знайдемо Радіан міру:
Давайте випишемо окремо кожну з цих функцій:
sin π 4 = sin 180 ∘ 4 = sin45 ∘ = 2 √ 2 \ sin \ frac \! \! \ pi \! \! \ text<>> = \ Sin \ frac ^ \ circ> = \ sin 45<>^ \ Circ = \ frac>
cos π 6 = cos 180 ∘ 6 = cos30 ∘ = 3 √ 2 \ cos \ frac \! \! \ pi \! \! \ text<>> = \ Cos \ frac ^ \ circ> = \ cos 30<>^ \ Circ = \ frac>
tg π 3 = tg 180 ∘ 3 = tg 60 ∘ = 3 √ tg \ frac \! \! \ pi \! \! \ text<>> = Tg \ frac ^ \ circ> = tg60<>^ \ Circ = \ sqrt
Тепер записуємо все три множника в єдину конструкцію для знаходження Радіан значення. Ось і все, ми отримали відповідь.
Переходимо до другого виразу і знайдемо Радіан міру:
Знову записуємо кожну функцію окремо:
cos π 3 = cos60 ∘ = 1 2 \ cos \ frac \! \! \ pi \! \! \ text<>> = \ Cos 60<>^ \ Circ = \ frac
ctg π 6 = ctg 30 ∘ = 3 √ ctg \ frac = ctg30<>^ \ Circ = \ sqrt
Знову збираємо всі отримані числа.
Як бачите, нічого складно в Радіан заходи кута немає. Якщо ця тема здасться вам занадто складною, просто запам'ятайте, що π \ pi рад = 180º, і всюди, де ви бачите π \ pi. можете сміливо писати 180º.
Ще одним важливим наслідком нового визначення тригонометричного кола є те, що синус, косинус і тангенс можуть бути негативними. Якщо раніше все зводилося до довжин катетів і гіпотенузи, то тепер перед нами абсциси і ординати якоїсь точки. При цьому пам'ятайте, що відкладання кута завжди йде в напрямку від осі Ox Ox до осі Oy Oy, причому йдеться саме про позитивні напрямках цих осей.
Щоб зрозуміти і назавжди запам'ятати, де знаходиться позитивний напрямок осі, просто пам'ятайте правило: туди, куди вказує стрілка при х і при у, це і є те саме позитивний напрямок осі.
- Безкоштовна підготовка до ЄДІ 7 простих, але дуже корисних уроків + домашнє завдання
