2.2. Моделювання за схемою безперервних марковських процесів
Існує широкий клас систем, які змінюють свої статки в випадкові моменти часу. Як і в попередньому випадку, в цих системах розглядається процес з дискретними станами. Наприклад, перехід об'єкта від справного стану до несправного, співвідношення сил сторін в ході бою і т. П. Оцінка ефективності таких систем визначається за допомогою ймовірностей кожного стану на будь-який момент часу,.
Щоб визначити ймовірності стану системи для будь-якого моменту часу необхідно скористатися математичними моделями марковських процесів з безперервним часом (безперервних марковських процесів).
При моделюванні стану систем з безперервними марковскими процесами ми вже не можемо скористатися перехідними ймовірностями, так як ймовірність "перескоку" системи з одного стану в інший точно в момент часу дорівнює нулю (як ймовірність будь-якого окремого значення неперервної випадкової величини).
Тому замість перехідних ймовірностей вводяться в розгляд щільності ймовірностей переходів:
де - ймовірність того, що система, яка перебувала в момент часу в стані за часом перейде в стан.
З точністю до нескінченно малих другого порядку з наведеної формули можна уявити:
Безперервний марковский процес називається однорідним, якщо щільності ймовірностей переходів не залежить від часу (від моменту початку проміжку). В іншому випадку безперервний марковский процес називається неоднорідним.
Метою моделювання. як і в разі дискретних процесів, є визначення ймовірностей станів системи. Ці ймовірності знаходяться інтеграцією системи диференціальних рівнянь Колмогорова.
Сформулюємо методику моделювання за схемою безперервних марковських процесів.
- Визначити стану системи і щільності ймовірностей переходів.
- Скласти і розмітити граф станів.
- Скласти систему диференціальних рівнянь Колмогорова. Число рівнянь в системі дорівнює числу станів. Кожне рівняння формується таким чином.
- B лівій частині рівняння записується похідна ймовірності -го стані.
- У правій частині записується алгебраїчна сума добутків і. Число творів стільки, скільки стрілок пов'язано з даними станом. Якщо стрілка графа спрямована в даний стан, то відповідний твір має знак плюс, якщо з даного стану - мінус.
- Визначити початкові умови і вирішити систему диференціальних рівнянь.
Приклад 2.2. Скласти систему диференціальних рівнянь Колмогорова для знаходження ймовірностей станів системи, розмічений граф станів якої представлений на рис. 2.3.
Мал. 2.3. Розмічений граф станів
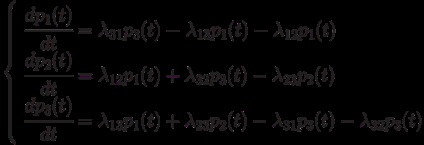
Тому будь-яка з перших трьох рівнянь можна виключити, як лінійно залежне.
Для вирішення рівнянь Колмогорова необхідно задати початкові умови. Для розглянутого прикладу 2.2, можна задати такі початкові умови:,.
При дослідженні складних об'єктів завжди цікавить: чи можливий в досліджуваній системі усталеною (стаціонарний) режим? Тобто, як поводиться система при? Чи існують граничні значення? Як правило, саме ці граничні значення цікавлять дослідника.
Відповідь на це питання дає теорема Маркова.
Якщо для однорідного дискретного марківського процесу з кінцевим або рахунковим числом станів все, то граничні значення існують і їх значення не залежать від обраного початкового стану системи.
Стосовно до безперервним марковским процесам теорема Маркова трактується так: якщо процес однорідний і з кожного стану можливий перехід за кінцеве час в будь-який інший стан і число станів лічильно або звичайно, то граничні значення існують і їх значення не залежать від обраного початкового стану.
Наприклад (рис. 2.4), в системі А стаціонарний режим є, а в системі В стаціонарного режиму немає: якщо система виявиться в стані вона не зможе перейти ні в який інший стан.
збільшити зображення
Мал. 2.4. Приклади графів станів систем з різними режимами
2.3. Схема загибелі і розмноження
Часто в системах самого різного призначення протікають процеси, які можна представити у вигляді моделі "загибелі і розмноження".
Граф станів такого процесу показаний на рис. 2.5.
Особливістю моделі є наявність прямого і зворотного зв'язків з кожним сусіднім станом для всіх середніх станів; перше і останнє (крайні) стану пов'язані тільки з одним "сусідом" (з подальшим і попереднім станами відповідно).
Назва моделі - "загибель і розмноження" - пов'язане з поданням, що стрілки вправо означають перехід до станів, пов'язаних з ростом номера стану ( "народження"), а стрілки вліво - до убування номера станів ( "загибель").
Очевидно, стаціонарний стан в цьому процесі існує. Складати рівняння Колмогорова немає необхідності, так як структура регулярна, необхідні формули наводяться в довідниках, а також в рекомендованій літературі.
Для наведених на рис. 2.5 позначень формули мають вигляд:
Приклад 2.3. Є система з двох однакових і працюють паралельно комп'ютерів.
Потрібно визначити надежностние характеристики цієї системи.