Зв'язний граф, незв'язних граф, компонента зв'язності, властивості
Неорієнтовані граф вважається зв'язковим, якщо з будь-якої вершини є шлях в будь-яку іншу вершину (шлях може складатися з будь-якої кількості ребер). Приклад: на малюнку трохи нижче граф є зв'язковим. Однак, скажімо, якщо видалити ребро між вершинами 4 і 5, то зв'язковим він не буде - з вершини 5 можна буде потрапити ні в яку іншу вершину.
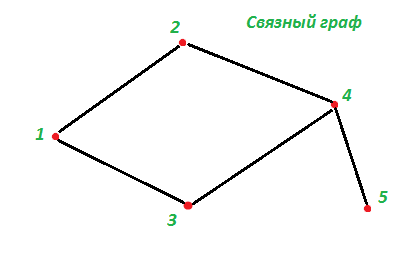
Якщо властивість зв'язності не виконується, граф називається незв'язних.
Далі ми не розглядаємо мультиграфом, тобто графи, у яких дві вершини можуть бути з'єднані двома і більше ребрами. Обмежимося розглядом графів, в яких кожна пара вершин або не з'єднана, або з'єднана єдиним ребром.
Щоб граф з n вершинами був зв'язковим, він повинен мати не менше (n -1) ребер.
Якщо граф має не менше (n * n - 3n + 4) / 2 ребер, то він гарантовано зв'язний.
Якщо граф зв'язний, у нього обов'язково є вершини ступеня не менше 2, тобто вершини, кожна з яких має не менше двох суміжних вершин.
Якщо граф зв'язний і без циклів (тобто це дерево), то видалення будь-якого ребра призведе до втрати зв'язності.
Незв'язний граф складається з компонент зв'язності. Компонента зв'язності - безліч вершин таке, що з будь-якої вершину цієї множини є шлях в будь-яку іншу вершину цієї множини, але ні з якої вершини цієї множини можна потрапити в деяку вершину поза цієї множини. Очевидно, що сума кількостей вершин компонент зв'язності дорівнює кількості вершин графа.
На малюнку наведено граф з двома компонентами зв'язності.
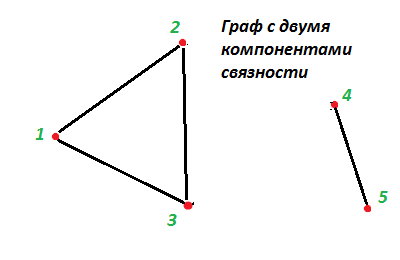
Зауважимо, що компонента зв'язності може складатися з однієї вершини. Якщо у графа n вершин, то він не може складатися з більш ніж n компонент зв'язності. У зв'язкового графа компонента зв'язності єдина.
У незв'язною графа будь-яка компонента зв'язності складається не більше, ніж з n -1 вершин. Якщо відомо, що у графа k компонент зв'язності, то даємо ще більш сувору оцінку: будь-яка компонента зв'язності складається з не більше, ніж з n-k +1 вершин.
Якщо у незв'язною графа k компонент зв'язності, то для отримання зв'язкового графа потрібно додати в граф як мінімум k -1 ребро.
Як визначити, чи є граф зв'язковим?
Вибираємо деяку вершину A і помічаємо її як відвіданих (1), інші відповідно покладаються ще не відвіданих (0):
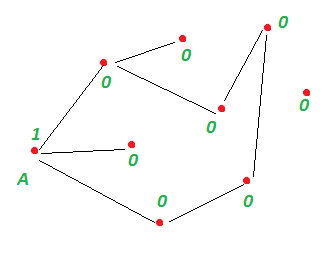
A вважаємо поточної вершиною. Далі діємо в такий спосіб. Позначка невідвіданих суміжних вершин: для поточної вершини шукаємо суміжні з нею, ще не невідвіданих, і помічаємо їх як відвідані.
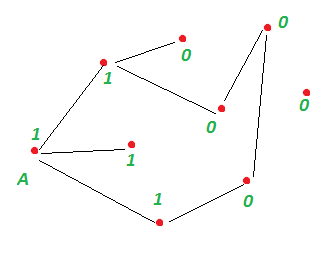
Нехай у нас виявилося k новопомеченних вершин (на малюнку трохи вище їх 3). По черзі вибираємо одну з них поточної і рекурсивно виконуємо позначку невідвіданих суміжних з нею вершин. Для поточної вершини не виконується рекурсія, якщо у даної вершини немає суміжних вершин, які все ще не позначені як відвідані.
Якщо після таких дій все вершини опиняться позначені як відвідані, граф зв'язний, інакше незв'язних.
Розберемо невеликий приклад:
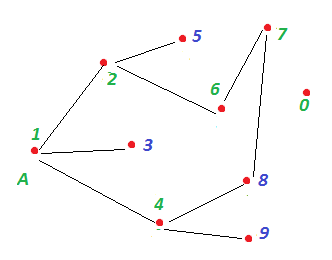
Тут натуральне число у вершини означає, який за рахунком вона була позначена як відвіданих, зелений колір числа означає, що для даної вершини був виконаний рекурсивний виклик.
Вибрали деяку вершину (1). Далі позначаються три суміжних з нею вершини (2, 3, 4). Поточної вершиною тепер стає (2). Рекурсія: помічаємо дві ще не відвідані суміжні вершини (номера 5 і 6). Для (5) рекурсія не потрібна - у неї немає невідвіданих суміжних вершин, для (6) рекурсія потрібна: помічаємо номер 7. У номера 7 є ще не відвіданих "сусід" - номер 8, а ось у номера 8 немає невідвіданих суміжних вершин. Все рекурсивні виклики, породжені з вершини (2), завершені. Тепер на черзі вершина (3), але тут немає необхідності рекурсії. Залишилася вершина (4). Одна з її суміжних вершин (9) ще не позначена, виправляємо це. Разом:
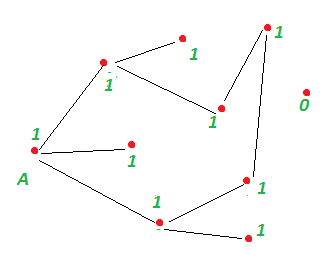
Висновок: не всі вершини відвідали, граф виявився незв'язним.