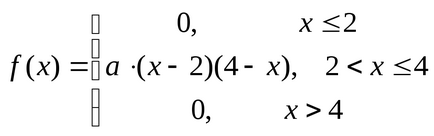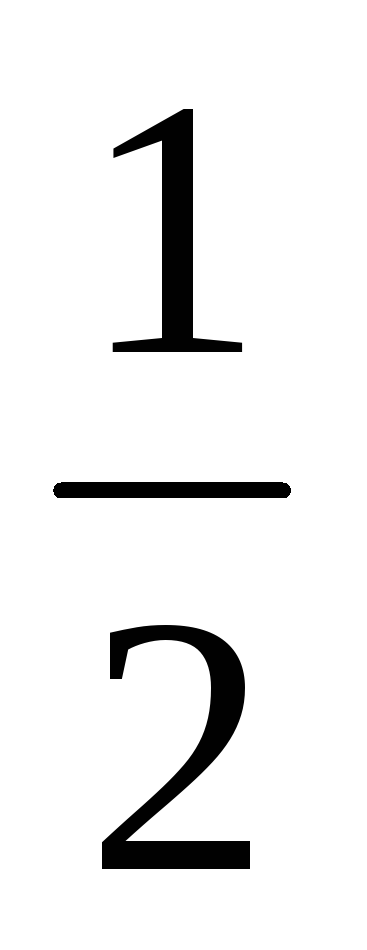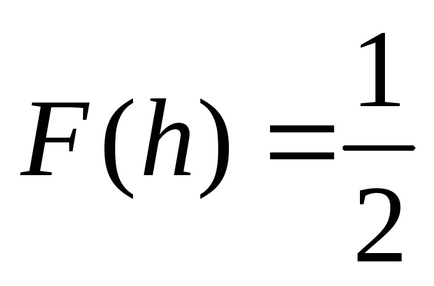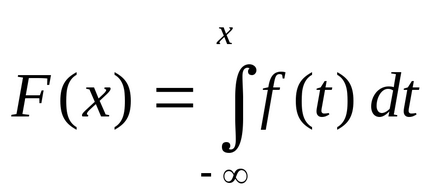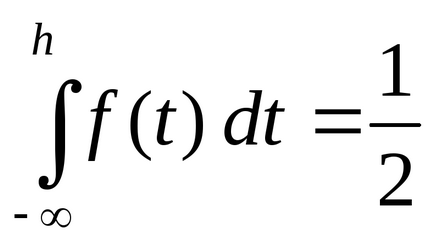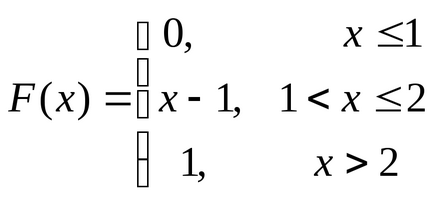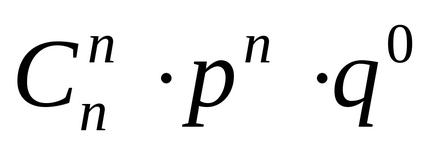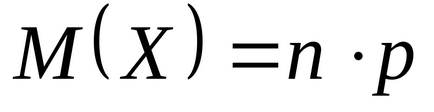Тоді її мода приймає 2 значення: d (Х) = 3 і d (Х) = 5.
Нехай Х - неперервна випадкова величина з щільністю ймовірності f (х). Модою цієї С.В. називається точка максимуму її щільності ймовірності. Ця точка максимуму функції f (x) знаходиться звичайними методами з використанням похідної.
Приклад. Дана щільність ймовірності н.с.в.
.
Знайти значення параметра а і моду цієї випадкової величини.
Нехай Х - неперервна випадкова величина. Медианой С.В. Х (позначається h (X)) називається таке число h. яке ділить всю числову пряму на 2 проміжку (-∞, h) та [h, + ∞). в які С.В. Х потрапляє з однаковою ймовірністю. Таким чином, якщо медіана h (X) = h, то виконується рівність
P (X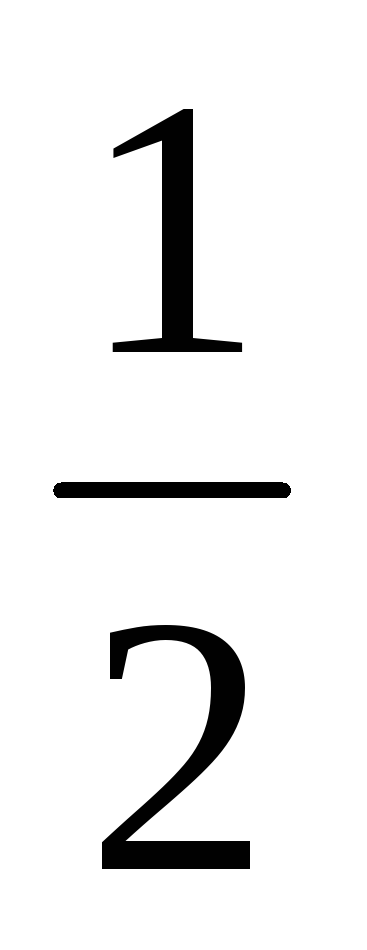
.
Згадуючи, що ймовірність P (X
.
Якщо ж у н.с.в. задана не функція розподілу F (x). а щільність ймовірності f (x). то згадуючи вираз функції розподілу через щільність ймовірності
. отримаємо, що значення h медіани задовольняє рівняння
.
Медіана h (X) безперервної С.В. Х шукається з одного з виписаних вище рівнянь (в залежності від того, що задано: F (x) або f (x)). Для дискретних випадкових величин медіана не визначається.
Приклад. Знайти медіану н.с.в. Х. заданої своєю функцією розподілу
.
Деякі важливі закони розподілу випадкових величин
Серед різних законів розподілу випадкових величин деякі зустрічаються в додатках найбільш часто. Тому для них отримані формули розрахунку їх числових характеристик: математичного очікування, дисперсії, моди, медіани і ряду інших. Розглянемо деякі з таких законів розподілу.
Біноміальний закон розподілу
Серед законів розподілу дискретних випадкових величин найбільш поширеним є біноміальний розподіл, з яким ми вже зустрічалися при розгляді так званої схеми Бернуллі (число появ деякої події в серії незалежних випробувань).
Дискретна випадкова величина Х розподілена за біноміальним законом. якщо вона приймає значення 0, 1, 2.n з вірогідністю р0, р1. рn. які обчислюються за формулою
,
де параметр розподілу р укладений між нулем і одиницею 0 ≤ р ≤ 1. а q = 1-p. Таким чином, д.с.в Х. розподілена за біноміальним законом, має наступний закон розподілу:
Як вже говорилося, за біноміальним законом розподілено число успіхів у схемі Бернуллі. Нехай проводиться n незалежних випробувань, в кожному з яких деяка подія А може з'явитися з однією і тією ж імовірністю р. Розглянемо С.В. Х - число появ події А в усіх n випробуваннях (те, що раніше називали число успіхів). Тоді С.В. Х розподілена за біноміальним законом. Ми вже знаходили формули для математичного очікування цієї випадкової величини, які і є формулами математичного очікування і дисперсії довільної випадкової величини, розподіленої за схемою Бернуллі:
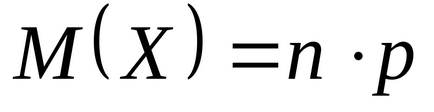
Знайдемо моду d (X) біноміальної розподіленої випадкової величини Х. тобто найімовірніше число успіхів у схемі Бернуллі. За визначенням моди d (X) = k. якщо ймовірність найбільша серед усіх ймовірностей р0, р1. рn. Знайдемо таке число k (це ціле невід'ємне число). При такому k ймовірність pk повинна бути не менше сусідніх з нею ймовірностей: pk-1≤pk≤pk + 1. Підставивши замість кожної ймовірності відповідну формулу, отримаємо, що число k має задовольняти подвійному нерівності:
.
Якщо розписати формули для числа сполучень і провести прості перетворення, можна отримати, що ліве нерівність дає k≤ (n + 1) ∙ p. а праве k≥ (n + 1) ∙ p-1. Таким чином, число k задовольняє подвійному нерівності (n + 1) ∙ p-1 ≤k≤ (n + 1) ∙ p. тобто належить відрізку [(n + 1) ∙ p-1, (n + 1) ∙ p]. Оскільки довжина цього відрізка, очевидно, дорівнює 1. то в нього може потрапити або одне, або 2 цілих числа. Якщо число (n + 1) ∙ p ціле, то в відрізку [(n + 1) ∙ p-1, (n + 1) ∙ p] є 2 цілих числа, що лежать на кінцях відрізка. Якщо ж число (n + 1) ∙ p не ціла, то в цьому відрізку є тільки одне ціле число.
Таким чином, якщо число (n + 1) ∙ p ціле, то мода біноміальної розподіленої випадкової величини Х приймає 2 сусідніх значення. d (X) = (n + 1) ∙ p-1 і d (X) = (n + 1) ∙ p. Якщо ж число (n + 1) ∙ p не ціла, то мода біноміальної розподіленої випадкової величини Х одне значення d (X) = k. де k є єдине ціле число, яке задовольняє нерівності (n + 1) ∙ p-1 ≤k≤ (n + 1) ∙ p. Якщо згадати, що запис [a] означає взяття цілої частини від числа а. то в цьому випадку можна записати d (X) = [(n + 1) ∙ p].
Приклад. Кубик підкидається 100 раз. Яке найімовірніше число випадінь шістки?
Приклад. Ймовірність влучення стрільцем в ціль дорівнює 0.7. Знайти найімовірніше число влучень в ціль при 30 пострілах.
Приклад. Імовірність виготовлення бракованої деталі на верстаті дорівнює 0.06. Яке найімовірніше число бракованих деталей в партії з 200 деталей, виточених на цьому верстаті?
Приклад. Банк видав 7 кредитів. Відомо, що в середньому не повертається 2 кредити з 10. Знайти середнє число неповернених кредитів.
Схожі статті