Шенягін А.С. БТСм-111
На сучасному етапі розвитку техніки, набагато зручніше і надійніше використовувати приймачі з цифровою обробкою сигналу. Оцифровка ВЧ-сигналу безпосередньо утруднена, так як сучасні цифрові схеми часто не має швидкодії, що задовольняє умовам теореми Котельникова-Шеннона. Вище було сказано, що в комплексній обвідної міститься вся необхідна інформація для декодування сигналу і обчислення його потужних і фазових характеристик. Комплексна огинає вузькосмугових сигналів являє собою пару низькочастотних сигналів, зручних для оцифровки (без порушення умов теореми Котельникова).
Для виделеніея з сигналу комплексної обвідної використовується процедура гетеродінірованія. Суть її полягає в наступному. Вхідний ВЧ-сигнал s (t) = A (t) ∙ cos (ω0 ∙ t + φ (t)) множиться на коливання двох генераторів (гетеродинов) з частотою ω0, зсунутих по фазі один відносно одного на кут π / 2 - cos (ω0 ∙ t) і -sin (ω0 ∙ t).
s (t) ∙ cos (ω0 ∙ t) = A (t) ∙ cos (ω0 ∙ t + φ (t)) ∙ cos (ω0 ∙ t) =
0,5 ∙ A (t) ∙ cos (φ (t)) + 0,5 ∙ A (t) ∙ cos (2ω0 ∙ t + φ (t)) =
s (t) ∙ (-sin (ω0 ∙ t)) = - A (t) ∙ cos (ω0 ∙ t + φ (t)) ∙ sin (ω0 ∙ t) =
0,5 ∙ A (t) ∙ sin (φ (t)) - 0,5 ∙ A (t) ∙ sin (2ω0 ∙ t + φ (t)) =
0,5 ∙ q (t) - 0,5 ∙ A (t) ∙ sin (2ω0 ∙ t + φ (t)) (2)
З формул (1) і (2) видно, що результати умножений містять дві складові - низькочастотну 0,5 ∙ i (t) і 0,5 ∙ q (t), які є дійсною і уявною частинами комплексної обвідної і високочастотну 0,5 ∙ A (t) ∙ cos (2ω0 ∙ t + φ (t)) і -0,5 ∙ A (t) ∙ sin (2ω0 ∙ t + φ (t)), які можуть бути прибрані фільтром низьких частот (ФНЧ) . На малюнках 1-2 представлені схеми квадратурного (векторного) демодулятора з фазовращателем і без фазовращателя.
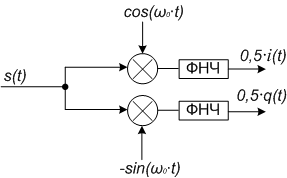
Малюнок 1 - Функціональна схема векторного демодулятора
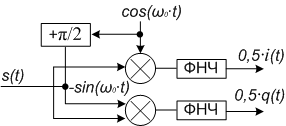
Малюнок 2 -Функціональна схема векторного демодулятора з фазовращателем
Векторний демодулятор описується формулами (1) і (2), які приймають такий "гарний" вид, лише в тому випадку, якщо опорний сигнал гетеродина повністю збігається за частотою і початковою фазою з опорним коливанням ω0 (тобто сигнал несучого коливання і гетеродина приймача когерентні). Дана умова може бути забезпечено за допомогою стежать систем, побудованих на основі схем фазового автопідстроювання частоти (ФАПЧ, PLL). Якщо ця умова не забезпечується, то на виході квадратурного демодулятора ми отримаємо дві компоненти з так званими биттям, частоти яких залежать від неузгодженості частоти гетеродина приймача і несучої частоти сигналу. Неузгодженість ж початкової фази гетеродина приймача і несучої частоти сигналу дасть спотворення за рівнями квадратурних проекцій. У цьому випадку говорять, що комплексна обвідна сигналу отримана щодо частоти ωg.
Опишемо математично дану ситуацію. Нехай частота гетеродина приймача дорівнює ωg = ω0 + δω, початкова фаза - φg. тоді:
s (t) ∙ cos (ωg ∙ t) = A (t) ∙ cos (ω0 ∙ t + φ (t)) ∙ cos (ωg ∙ t + φg) =
A (t) ∙ 0,5 ∙ cos (ω0 ∙ t + φ (t) + ωg ∙ t + φg) + A (t) ∙ 0,5 ∙ cos (ω0 ∙ t + φ (t) - ωg ∙ t -φg) = ...
Згрупуємо доданки під косинусом, виділивши окремо доданок φ (t) і розкладемо по формулам складання аргументів:
= A (t) ∙ 0,5 ∙ cos (φ (t)) ∙ cos ((ω0 + ωg) ∙ t + φg) -.
-A (t) ∙ 0,5 ∙ sin (φ (t)) ∙ sin ((ω0 + ωg) ∙ t + φg) + ...
+A (t) ∙ 0,5 ∙ cos (φ (t)) ∙ cos ((ωg - ω0) ∙ t + φg) + ...
+A (t) ∙ 0,5 ∙ sin (φ (t)) ∙ sin ((ωg - ω0) ∙ t + φg) = ...
Так як ωg = ω0 + δω
= A (t) ∙ 0,5 ∙ cos (φ (t)) ∙ cos ((2 ∙ ω0 + δω) ∙ t + φg) -.
-A (t) ∙ 0,5 ∙ sin (φ (t)) ∙ sin ((2 ∙ ω0 + δω) ∙ t + φg) +.
+ A (t) ∙ 0,5 ∙ cos (φ (t)) ∙ cos (δω ∙ t + φg) + ...
+ A (t) ∙ 0,5 ∙ sin (φ (t)) ∙ sin (δω ∙ t + φg) = ...
= 0,5 ∙ i (t) ∙ cos ((2 ∙ ω0 + δω) ∙ t + φg) -.
-0,5 ∙ q (t) ∙ sin ((2 ∙ ω0 + δω) ∙ t + φg) + ...
+0,5 ∙ i (t) ∙ cos (δω ∙ t + φg) + ...
+0,5 ∙ q (t) ∙ sin (δω ∙ t + φg)
Після ФНЧ маємо
Ib (t) = 0,5 ∙ i (t) ∙ cos (δω ∙ t + φg) + 0,5 ∙ q (t) ∙ sin (δω ∙ t + φg)
s (t) ∙ sin (ωg ∙ t) = A (t) ∙ cos (ω0 ∙ t + φ (t)) ∙ sin (ωg ∙ t + φg) =.
A (t) ∙ 0,5 ∙ sin (ω0 ∙ t + φ (t) + ωg ∙ t + φg) + A (t) ∙ 0,5 ∙ sin (ωg ∙ t + φg - ω0 ∙ t -φ ( t)) =.
Згрупуємо доданки під косинусом, виділивши окремо доданок φ (t) і розкладемо по формулам складання аргументів:
= A (t) ∙ 0,5 ∙ sin (φ (t)) ∙ cos ((ω0 + ωg) ∙ t + φg) +.
+ A (t) ∙ 0,5 ∙ cos (φ (t)) ∙ sin ((ω0 + ωg) ∙ t + φg) +.
+ A (t) ∙ 0,5 ∙ cos (φ (t)) ∙ sin ((ωg - ω0) ∙ t + φg) - ...
- A (t) ∙ 0,5 ∙ sin (φ (t)) ∙ cos ((ωg - ω0) ∙ t + φg) = ...
Так як ωg = ω0 + δω
= A (t) ∙ 0,5 ∙ sin (φ (t)) ∙ cos ((2 ∙ ω0 + δω) ∙ t + φg) +.
+A (t) ∙ 0,5 ∙ cos (φ (t)) ∙ sin ((2 ∙ ω0 + δω) ∙ t + φg) +.
+ A (t) ∙ 0,5 ∙ cos (φ (t)) ∙ sin (δω ∙ t + φg) -.
- A (t) ∙ 0,5 ∙ sin (φ (t)) ∙ cos (δω ∙ t + φg) =.
= 0,5 ∙ q (t) ∙ cos ((2 ∙ ω0 + δω) ∙ t + φg) +.
+0,5 ∙ i (t) ∙ sin ((2 ∙ ω0 + δω) ∙ t + φg) +.
+ 0,5 ∙ i (t) ∙ cos (δω ∙ t + φg) -.
- 0,5 ∙ q (t) ∙ sin (δω ∙ t + φg)
= - 0,5 ∙ q (t) ∙ cos ((2 ∙ ω0 + δω) ∙ t + φg) -.
- 0,5 ∙ i (t) ∙ sin ((2 ∙ ω0 + δω) ∙ t + φg) -.
- 0,5 ∙ i (t) ∙ cos (δω ∙ t + φg) +.
+ 0,5 ∙ q (t) ∙ sin (δω ∙ t + φg)
Після ФНЧ маємо
Qb (t) = 0,5 ∙ q (t) ∙ cos (δω ∙ t + φg) - 0,5 ∙ i (t) ∙ sin (δω ∙ t + φg)
Таким чином, на виході квадратурного демодулятора маємо два сигнали
Ib (t) = 0,5 ∙ i (t) ∙ cos (δω ∙ t + φg) + 0,5 ∙ q (t) ∙ sin (δω ∙ t + φg) (3)
Qb (t) = 0,5 ∙ q (t) ∙ cos (δω ∙ t + φg) - 0,5 ∙ i (t) ∙ sin (δω ∙ t + φg) (4)