Визначення 1.Функция алгебри логікіnпеременних називається будь-яка функція n змінних, аргументи якої приймають два значення 1 і 0, і сама функція приймає одне з двох значень: 1 або 0.
Будь-яка формула алгебри логіки є функція алгебри логіки. Тотожно істинна і то тотожне помилкова формули є постійні функції.
Можна показати, що будь-яку функцію алгебри логіки можна представити у вигляді формули логіки, і це уявлення таке:
(*)
Формулу (*) можна перетворити до формули, яка містить тільки елементарні змінні висловлювання і має такі властивості досконалості (або властивостями (С)):
1) кожне логічне доданок формули містить всі змінні, що входять в функцію;
2) всі логічні складові формули різні;
3) жодне логічне доданок формули не містить одну і ту ж змінну і її заперечення;
4) жодне логічне доданок формули не містить одну і ту ж змінну двічі.
За допомогою таблиці істинності, що визначає функцію, легко отримати відповідну формулу алгебри логіки, що володіє властивостями (С). Дійсно, для кожного набору значень змінних на якому функція приймає значення 1, запишемо кон'юнкцію елементарних змінних висловлювань, взявши за член кон'юнкції
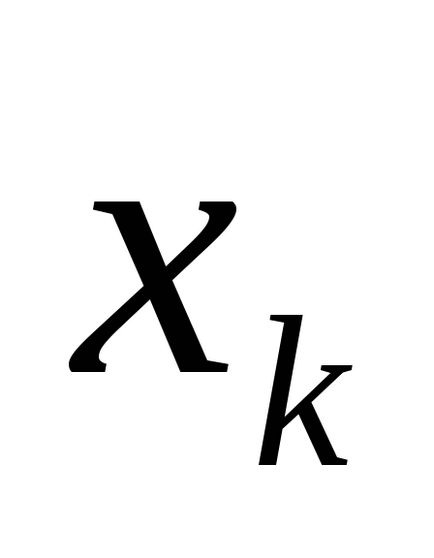
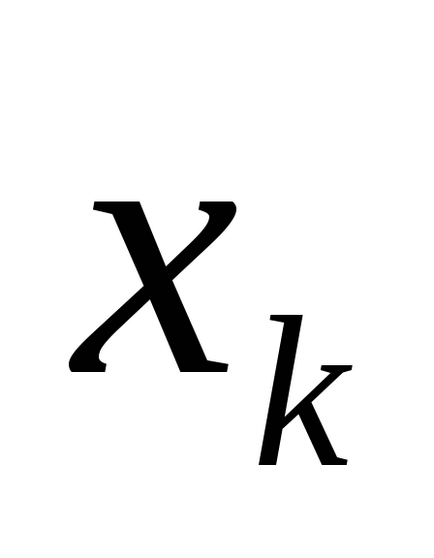
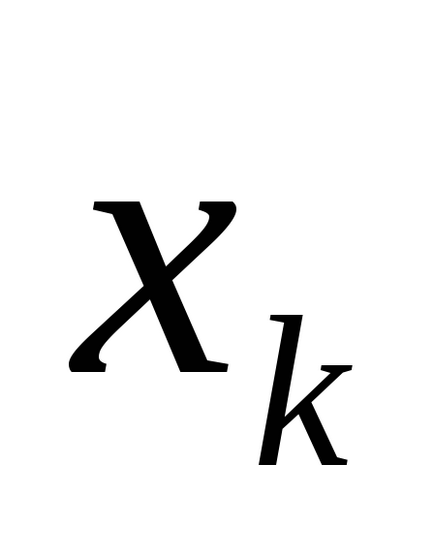
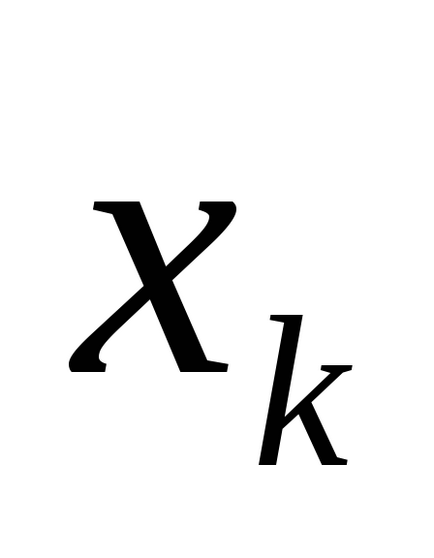
Визначення 2.Елементарной кон'юнкціейn змінних називається кон'юнкція змінних або їх заперечень.
Визначення 3. диз'юнктивного нормальною формою (ДНФ) формули A називається рівносильна їй формула, що представляє собою диз'юнкцію елементарних кон'юнкції.
Визначення 4.Совершенной диз'юнктивній нормальною формою (СДНФ) формули A називається ДНФ A. володіє властивостями (С).
СДНФ A можна отримати двома способами: а) за допомогою таблиці істинності (див. Вище); б) за допомогою рівносильних перетворень.
Правило отримання СДНФ з формулиA за допомогою рівносильних перетворень.
1. Для формули A отримуємо будь-яку ДНФ.
2. З ДНФ A шляхом рівносильних перетворень отримуємо СДНФ, послідовно домагаючись виконання чотирьох властивостей СДНФ:
1) Нехай B є доданок ДНФ, що не містить
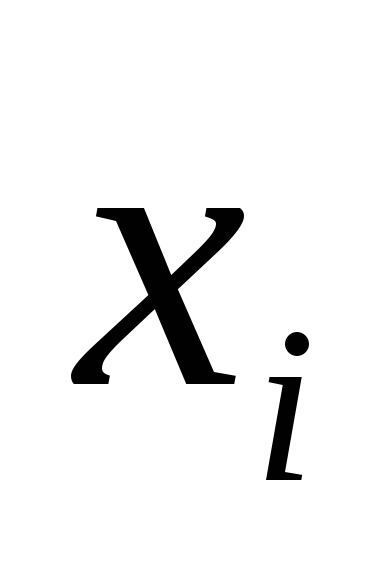
2) Якщо в ДНФ A зустрінеться два неоднакових доданків

3) Якщо в якийсь доданок B в ДНФ A змінна

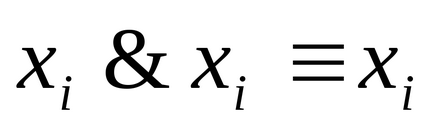
4) Якщо доданок B в ДНФ A містить кон'юнкцію
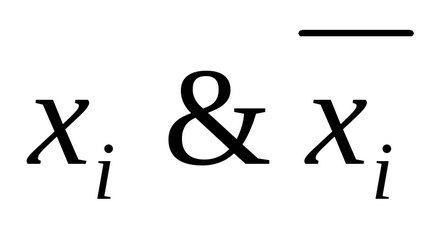
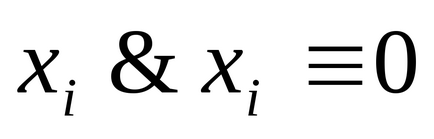
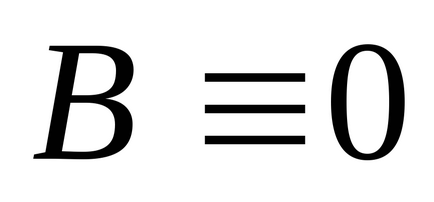
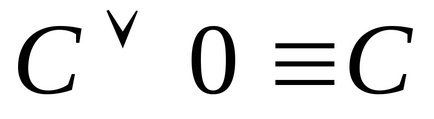
Визначення 5.Елементарной діз'юнкціейn змінних називається диз'юнкція змінних або їх заперечень.
Визначення 6.Кон'юнкція нормальною формою (КНФ) формули А називається рівносильна їй формула, що представляє собою кон'юнкцію елементарних диз'юнкцій.
Визначення 7.Совершенной кон'юнктівной нормальною формою формули А (СКНФ А), називається КНФ А. задовольняє чотирьом властивостям:
1) всі елементарні диз'юнкції, що входять до КНФ А. містять всі змінні;
2) все елементарні диз'юнкції, що входять до КНФ А. різні;
3) кожна елементарна диз'юнкція, що входить в КНФ А. містить змінну один раз;
4) жодна елементарна диз'юнкція, що входить в КНФ А. не містить змінну і її заперечення.
СКНФ А можна отримати двома способами: а) за допомогою таблиці істинності (використовуючи закон подвійності, отримуємо за допомогою таблиці істинності
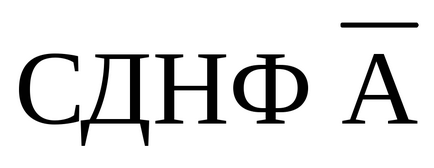
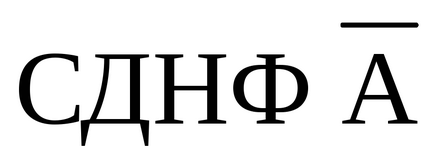
Правило отримання СКНФ з формулиА за допомогою рівносильних перетворень.
1. Для формули А отримуємо будь-яку КНФ.
2. З КНФ А шляхом рівносильних перетворень отримуємо СКНФ А. послідовно домагаючись виконання чотирьох властивостей СКНФ.
1) Якщо елементарна диз'юнкція В. входить в КНФ А. не містить змінну
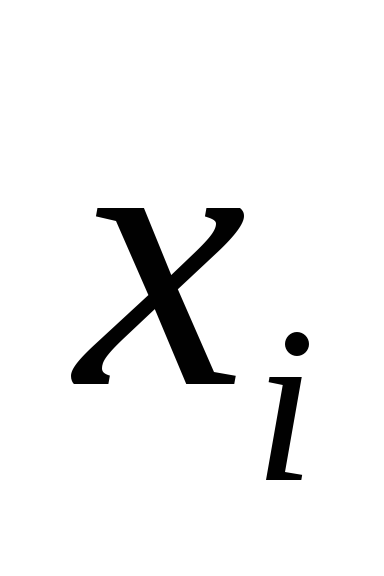
2) Якщо в деяку елементарну диз'юнкцію В змінна
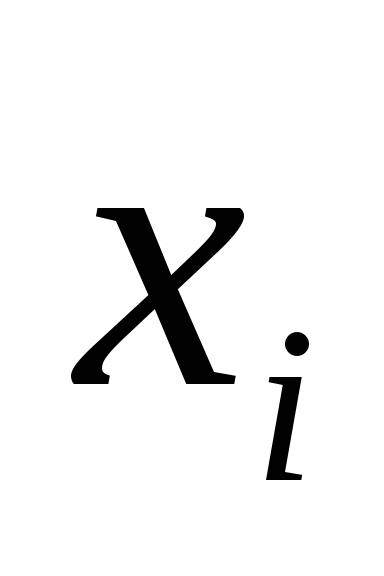
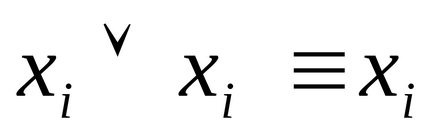
3) Якщо КНФ А містить дві однакових елементарних диз'юнкції, то одну можна відкинути, так як
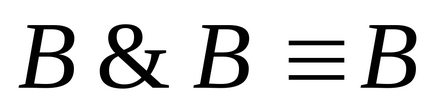
4) Якщо в елементарну диз'юнкцію входить пара
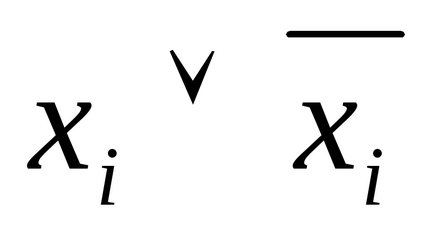
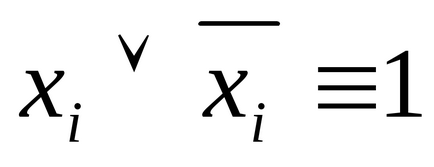
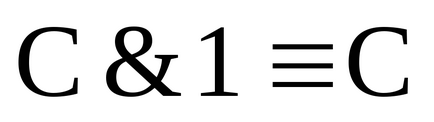
Приклад 1. Знайти формулу, визначальну функцію Ф (x, y, z), по заданій таблиці істинності:
Рішення. Використовуючи правило отримання формули алгебри логіки з таблиці істинності для функції Ф (x, y, z), отримаємо:
.
Спростивши цю формулу, отримаємо:
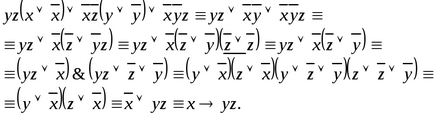
Таким чином, шуканої формулою, що визначає функцію Ф (x, y, z), можна вважати
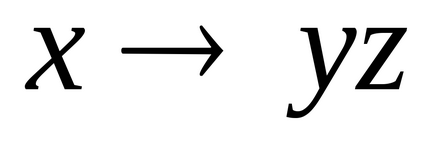
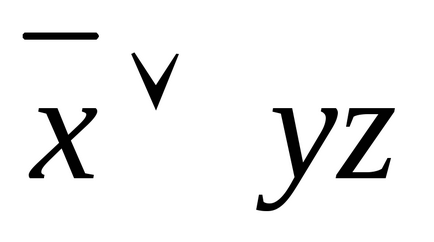
Приклад 2. Наступну формулу привести до СДНФ, попередньо привівши її рівносильними перетвореннями до ДНФ:.
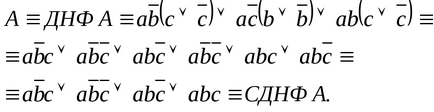
Приклад 3. Для формули з прикладу 2 знайти СДНФ шляхом складання таблиці істинності.
Рішення. Складемо таблицю істинності для формули.
Приклад 4. Для формули з прикладу 2 знайти СКНФ шляхом рівносильних перетворень, попередньо привівши її до КНФ.
Рішення. З прикладу 2: .Далі
.
Приклад 5. Для формули з прикладу 2 знайти СКНФ, записавши попередньо ДНФ її заперечення, а потім скориставшись формулою подвійності.
Всі формули алгебри логіки діляться на три класи: 1) тотожне повну довіру; 2) тотожно хибні; 3) здійсненні.
Формулу А називають здійсненним. якщо вона приймає значення 1 хоча б на одному наборі значень вхідних в неї змінних і не є тотожним істиною.
Теореме.Для того, щоб формула алгебри логіки була тотожно істинна (помилкова), необхідно і достатньо будь-яка елементарна диз'юнкція (сполучення), що входить в КНФ А (ДНФ А), містила змінну і її заперечення.
Приклад 6. Чи буде формула тотожно істинною, тотожне помилковою або здійсненним?
Рішення. Наведемо приклад до будь-якої нормальної формі:
Отримання ДНФ не є тотожно хибною, оскільки кожна елементарна кон'юнкція не містить змінну і її заперечення. Отже, вихідна формула тотожно істинна або здійсненна. Перетворимо цю формулу до КНФ.
Цей твір не є тотожно істинним, так як елементарна сума
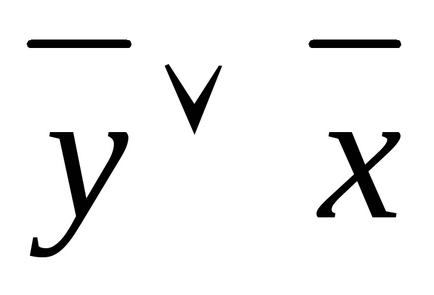
1.34. По таблиці істинності знайдіть формули, що визначають функції
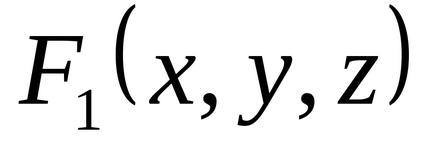
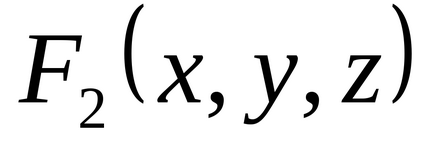
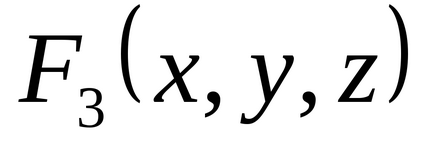
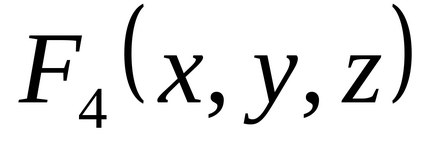
1.35. нехай
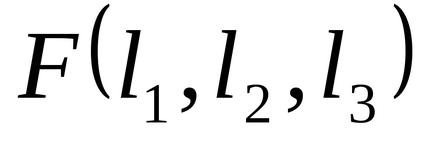
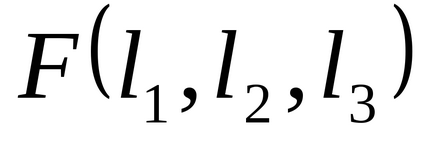
1.36. Назвемо функцією більшості
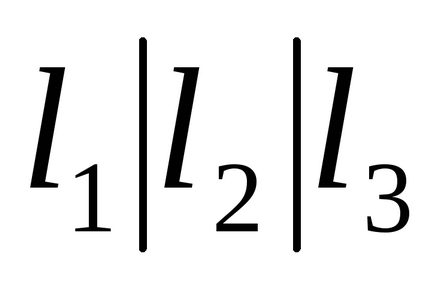
а) Складіть таблицю, що визначає функцію більшості і висловіть цю функцію через основні операції.
б) Спростіть вираз
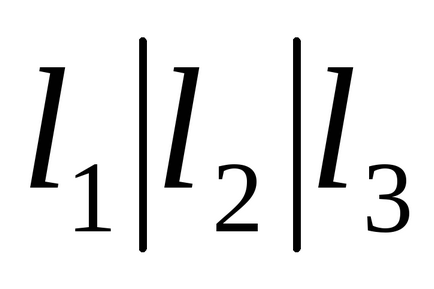
1.37. булева функції
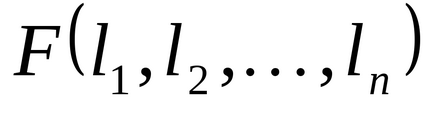
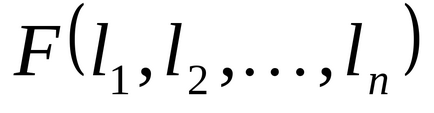
.
Для кожної булевої функції від двох змінних знайдіть двоїсту їй булеву функцію.
1.38. булева функції
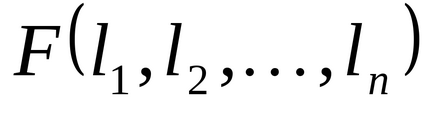
а) зберігає 0, якщо;
б) зберігає 1, якщо.
Серед булевих функції від однієї і двох змінних знайти всі функції, що зберігають 1, і всі функції, що зберігають 0.
1.39. Для наступних формул знайти СДНФ і СКНФ, кожну двома способами (шляхом равносильности перетворень і використовуючи таблиці істинності):
1.40. Знайдіть СДНФ для всякої тотожно істинною формули, що містить: 1) одне змінне, 2) два змінних, 3) три змінних.
1.41. Знайдіть СКНФ для будь-якої тотожно істинною формули, що містить: 1) одне змінне, 2) два змінних, 3) три змінних.
1.42. Доведіть равносильность формул
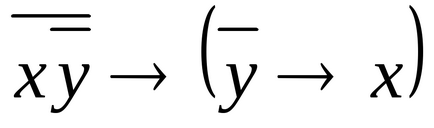
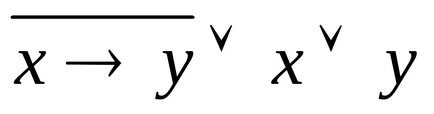
1.43. Знайдіть найбільш простий вид формул, що мають такі досконалі нормальні форми:
1.44. Використовуючи критерій тотожною істинності і тотожної хибності формули, встановити чи буде дана формула тотожно істинною, тотожне помилковою або здійсненним: