Теорема 2. Площина, що не проходить через вершину прямого кругового конуса, перетинає його по еліпсу, якщо вона перетинає всі твірні конуса (Див. Ріс.190), по параболі, якщо вона паралельна тільки однієї котра утворює конуса (Див. Ріс.191) і по гіперболі, якщо вона паралельна двом утворюючим конуса (Див. ріс.192).
Доведення. Для доказу розглянемо прямий круговий конус, який в прямокутній системі координат описується рівнянням:
і геометрично виходить при обертанні навколо осі прямої. що належить координатної пло-кістки. В силу кругової симетрії поверхні (6) можна обмежитися тільки перетинами при помо-щи площин, перпендикулярних координатної пло-скостити. Таким площинах відповідають рівняння. .
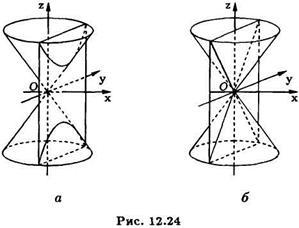
Якщо. то січна площина описується рівнянням. де і паралельна координатній площині. Підставивши значення абсциси в рівняння конуса (6), знайдемо, що перетин в площині описується рівнянням і при визначає собою рівносторонній гіперболи (Див. Ріс.12.24), а при пару прямих, які є складовими конуса. Ріс.12.24.
Нехай тепер в рівнянні січної площини коефіцієнт. Тоді площину можна представити рівнянням. де. . В силу симетрії конуса відносно площини досить обмежитися випадком, коли.
Конічний перетин для даної площини в просторі буде описуватися системою двох рівнянь (7)
Щоб отримати рівняння січної площини, розглянемо прямокутну систему координат,
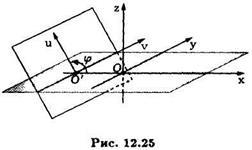
взявши в якості координатних осей і прямі, що є перетином січної площини з координатними площинами і (див.рис. 12.25).
Координати і довільної точки в січної площини будуть пов'язані з її координатами. і в просторі співвідношеннями:
де - кут між конічним перетином, перпендикулярним координатної площини. і координатної площиною. причому. а.
Підставляючи (8) в перше рівняння системи (7), тобто в рівняння. отримаємо рівняння конічного перетину в системі координат:
. Розкриваючи дужки і приводячи подібні члени, знаходимо:
При. коли січна площина утворює з площиною той же кут, що й утворюють конуса, конічні перетину будуть являти собою параболи (Див. мал.) і описуватися рівнянням:
Варіюючи параметр в рівнянні січної площини, як конічного перетину можна отримати будь-яку параболу.
При. рівняння (9) набуває вигляду:
Тут можливі два варіанти. При. тобто коли січна утворює з площиною менший кут, ніж утворюють конуса, буде виконано нерівність і тому рівняння (10) конічного перетину буде рівнянням еліпса (Див. мал. 12.26).
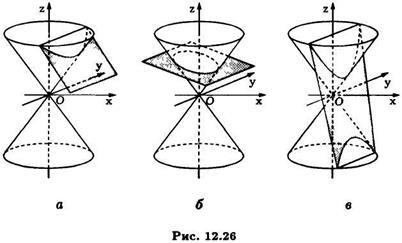
І тут варіюючи параметри і в рівнянні січної площини, ми можемо отримати в перерізі будь еліпс.
При. тобто коли січна площина утворює з площиною більший кут, ніж утворюють конуса, маємо. так що конічний перетин, що описується рівнянням (10) буде гіперболою (Див. мал.). Варіюючи параметри і можна отримати в конічному перетині будь-яку гіперболу.